How many clues do you need for a Sudoku puzzle?
Our Sudoku puzzles have between 24 and 32 clues, depending on the difficulty of the puzzle. But, how many clues do you need for a Sudoku that has a unique solution? This question has puzzled Sudoku enthusiasts for a long time.
When Sudoku exploded in popularity in around 2006, there was some research carried out to investigate this problem. A Sudoku researcher by the name Gordon Royle found a set of Sudoku starting grids that only had 17 clues (while still having only one solution). Gordon Royle maintained a list of 17-clue Sudoku puzzles, and invited enthusiasts to send him 16 clue grids that had a unique solution. Gordon never received a starting Sudoku with only 16 clues, but did that mean that they didn't exist?
In 2009, a group of three researchers began in earnest to try to prove a Sudoku grid had to have a minimum of 17 clues. The problem with Sudoku is the size of the problem. There are 6,670,903,752,021,072,936,960 different filled Sudoku grids, how would you go about proving that none of those grids have a 16-clue starting grid?
There are a few things that can be done to reduce the number of Sudoku grids that need to be considered in this hunt. Take these two completed grids,
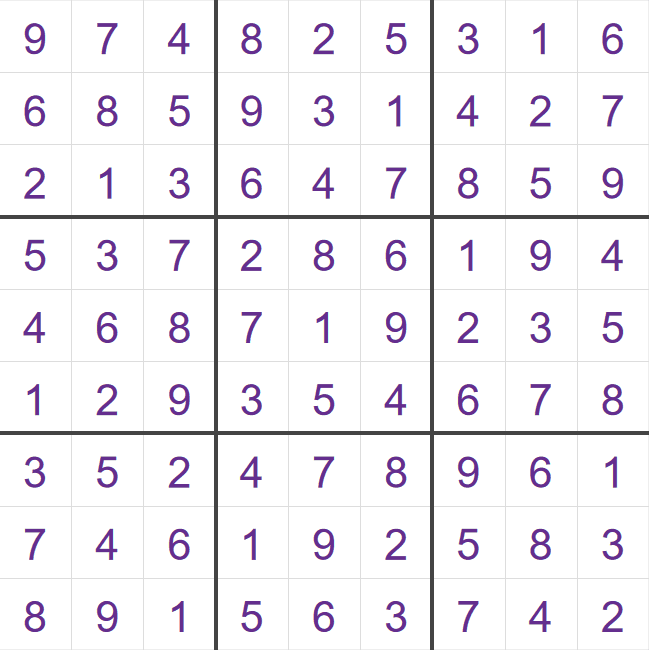
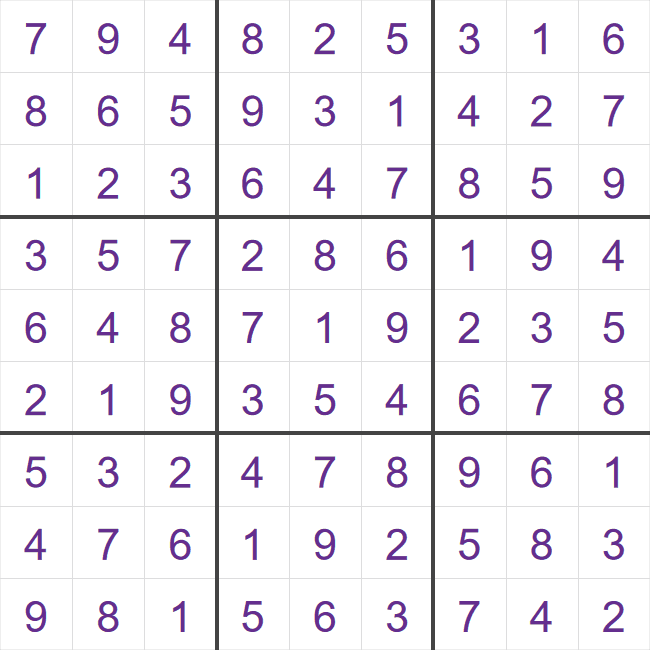
You will notice that these two grids are essentially the same grid - the first and second columns have been swapped. This doesn't have any impact on the solvability of any starting grid for this completed grid - the steps and techniques would be identical in both cases, i.e. if there is a valid 16-clue starting grid for the grid on the left, there will also be one for the grid on the right. This means the research team only needed to consider one of these two grids.
These two grids are also essentially the same,

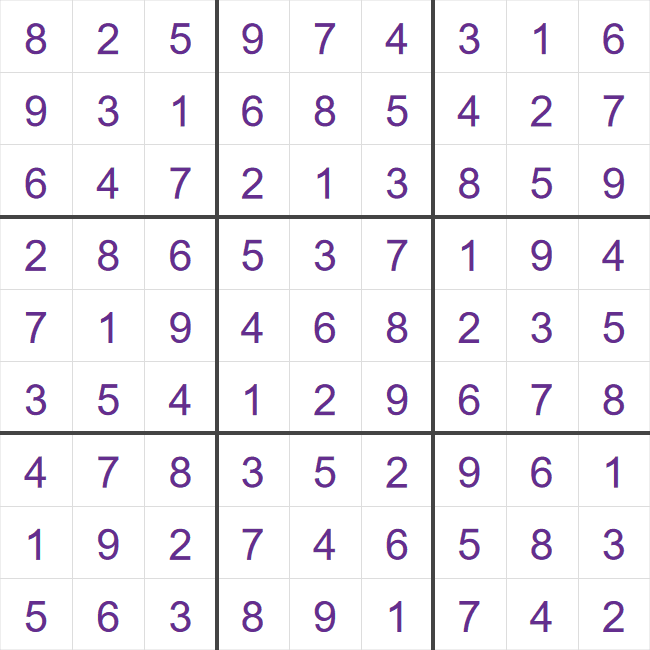
In this example, we have swapped the 1st, 2nd and 3rd columns with the 4th, 5th and 6th columns. These two grids are also essentially the same.
This is a little more subtle, but these two grids are also essentially the same,

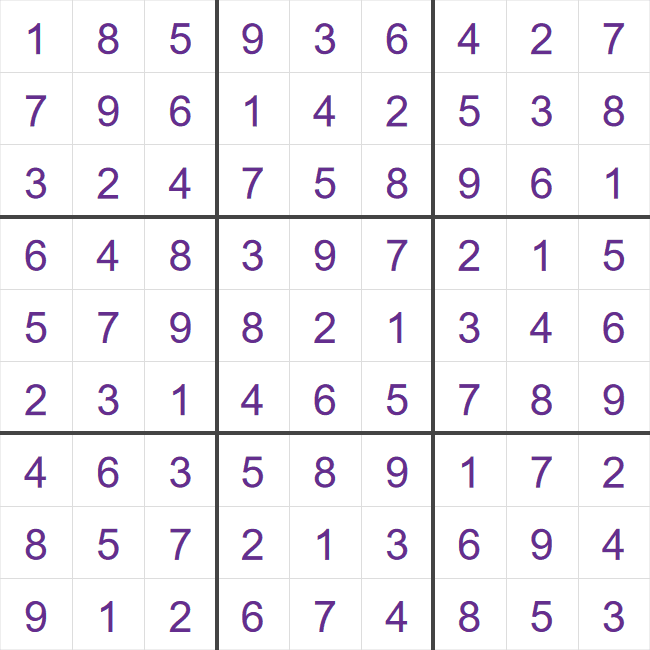
In this case, we have added 1 to every number (a '9' becomes a '1'). Again, if there is 16-clue starting grid for the first grid, there will also be one for the second grid, so the research team didn't need to consider both of these grids.
All of these techniques can be combined together to significantly reduce the number of 'essentially different' groups of filled Sudoku grids. The only technique we haven't looked at is the rotation and transposition of the grid. By applying and combining these techniques, the research team arrived at 5,472,730,538 essentially different groups of filled Sudoku grids. This is much more manageable than the original 6,670,903,752,021,072,936,960 grids!
The next problem the research team encountered was, for a given filled Sudoku grid, how many 16-clue starting grids are there? The answer is 33,594,090,947,249,085, for a single filled grid. Multiply this by the 5,472,730,538 essentially different filled grids, and this is a huge number of possible 16-clue starting grids to consider!
The team looked at what is called "Unavoidable Sets". Look at the puzzle below, there are two highlighted sets of cells.
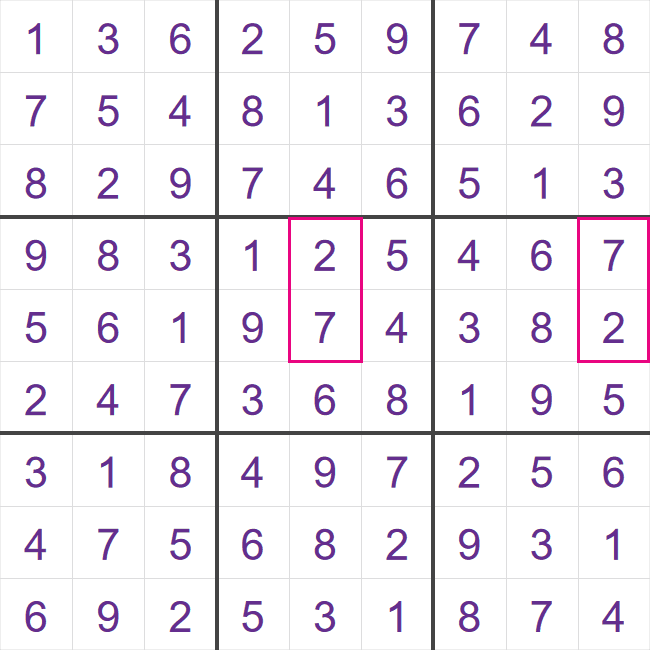
We can see here that we can swap these two sets of cells, and still have a valid completed Sudoku. This means that for starting grids for this completed grid, at least one of these 4 highlighted cells must be given. If this was not the case, then our starting grid would have at least two different solutions, i.e. it would not be a valid 16-clue Sudoku.
This completed grid has multiple unavoidable sets, and you will sometimes find unavoidable sets that has 3 cells instead of 2. Taking advantage of this situation allowed the research team to dramatically reduce the number of possible 16-clue starting grids for each filled grid they needed to consider.
The exact number of unavoidable sets each completed grid has varies from grid to grid. Some completed grids will have a large number of unavoidable sets, others will have very few.
By looking only at essentially different grids, and unavoidable sets, the team had brought the size of the problem down to a more manageable size. But, they were still left with a large computational task to complete. They needed to take every possible 16-clue starting grid for each candidate filled grid, and see if they were able to solve the puzzle from that starting position.
They chose to use an existing open source Sudoku solver called BBSudoku. BBSudoku solved a Sudoku puzzle in the same way a human person would, i.e. it would look for naked singles, hidden singles, locked candidates, before moving on to more advanced techniques such as X-Wing, Swordfish etc. After exhausting all of these logic-based techniques, it would finally take a brute-force approach, i.e. try a number in a cell, and see if that gives a valid completed grid.
The aims of the research teams was to solve (or not) each 16-clue grid as quickly as possible. They didn't care how the solver arrived at the solution. With this in mind, they found that the solver was quickest when it didn't use the advanced solving techniques, and jumped earlier to a brute-force approach. It was fastest when applying the naked singles, hidden singles, locked candidates techniques, etc, skip techniques such as X-Wing and Swordfish, and jump directly to a brute force approach. In the end, the solver was able to check over 50,000 16-clue candidate grids for a unique solution every second.
To perform the computations required, the research team were able to acquire time on a super computer at the Irish Centre for High-End Computing. The computation started in January 2011 and was completed in December 2011. The conclusion? There wasn't a single 16-clue Sudoku starting grid with a unique solution.
The full paper can be read here.
What about Sudoku variants?
It's true that there isn't a 16-clue starting grid with a unique solution, but what about a Sudoku variant? With the possible exception of Jigsaw Sudoku, all of the other variants place more restrictions on the placement of clues. In turn, this means that fewer starting clues are needed.
If you were to look at our X-Sudoku puzzles, you will notice that our X-Sudoku puzzles have fewer starting clues than our Sudoku puzzles (assuming the difficulty level is the same). X-Sudoku place another restriction, but it's not a severe restriction - there is plenty of possibilities when inserting numbers. This means the number of starting clues is only slightly lower for a X-Sudoku grid.
If you were to look at something like an Arrow Sudoku puzzle, that is a much more severe restriction - some of our tough Arrow Sudoku puzzles only have 5 starting clues! That is a massive reduction from the 22 or so clues our Tough Sudoku puzzles will have.
The follow-up question might then be, what is the minimum number of clues needed for a X-Sudoku, Hyper Sudoku, Arrow Sudoku, etc grid? It's unlikely there will ever be enough interest in these variants for that question to be answered.
It has to be remembered that the research team that looked at the case for vanilla Sudoku puzzles were not looking at this problem in isolation. Some work had already been done in terms of looking at essentially different Sudoku grids, at Unavoidable sets, and at writing a fast solver. Without this work, the problem could not have been reduced to one that could be completed in a reasonable time-frame.
This work hasn't been done for the other Sudoku variants (to my knowledge). This means that anybody wanting to investigate a similar question for Sudoku variants would need to complete this groundwork themselves. Also, the amount of interest in Sudoku is lower than it was in 2011 - securing time on a super computer to investigate the 16-clue standard Sudoku problem would be harder now. Securing time on a super-computer to investigate a Sudoku variant would be harder.
What about bigger Sudoku grids?
The question of how many starting clues are required for a 16x16 Sudoku is a much harder problem to solve. The problem with many of these types of logic puzzles is that when you are performing calculations for the number of possibilites, they very often involve factorials.
If we consider an individual row in a standard Sudoku grid, we have 9 numbers we need to insert in 9 cells. The number of ways we can do this is given by,
Conclusion
It's clear that there isn't a 16-clue Sudoku with a unique solution. Beyond that, we don't know the minimum number of clues for any other type of Sudoku variant - size or otherwise. As for Sudoku variants, there isn't enough interest, and it's unlikely this question will ever be answered.
We hope you enjoyed reading this article! Is there anything else you would like us to write about? Let us know!