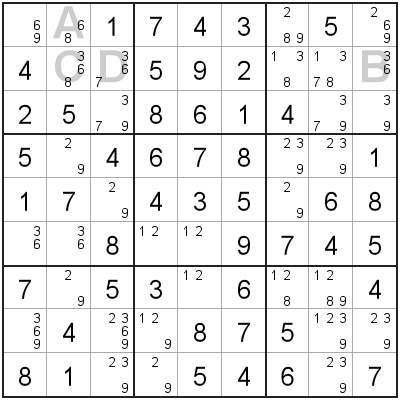
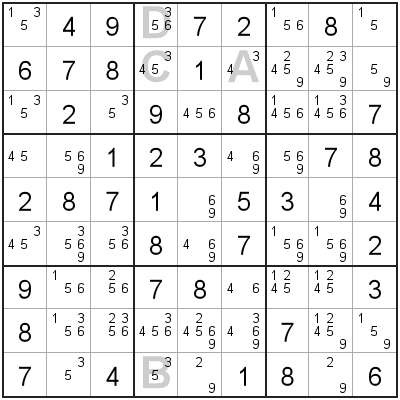
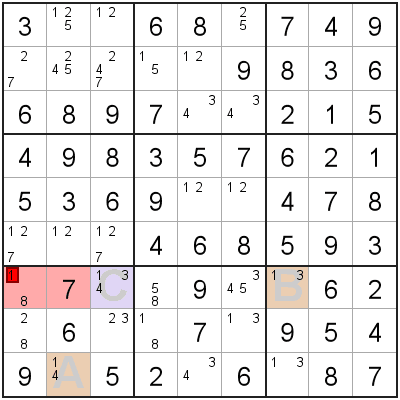
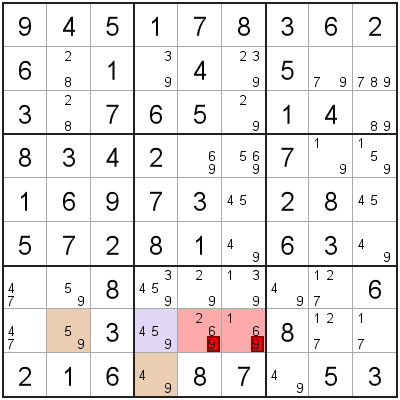
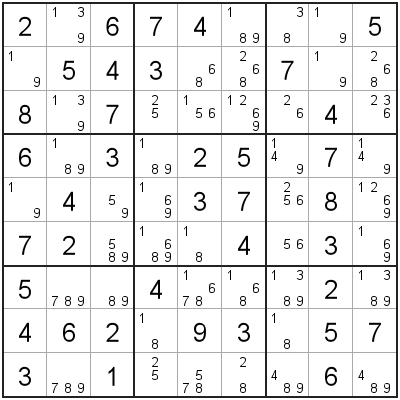
XYZ-Wing

This is an example of a situation where we can apply XYZ-Wing.

Let's imagine that we inserted the value '6' in Cell D,

⇒ Cell A would have the value '8'.

⇒ Cell B would have the value '3'.

⇒ This would leave no remaining candidates for cell C, i.e. an invalid state.

⇒ This means we can remove the '6' candidate from cell D.

This is another example of a situation where we can apply XYZ-Wing.

Let's imagine that we inserted the value '3' in Cell D,

⇒ Cell A would have the value '4'.

⇒ Cell B would have the value '5'.

⇒ This would leave no remaining candidates for cell C, i.e. an invalid state.

⇒ This means we can remove the '3' candidate from cell D.

When looking for situations where you can apply XYZ-Wing, you are looking for,

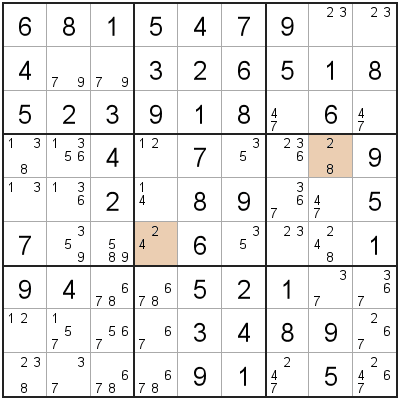
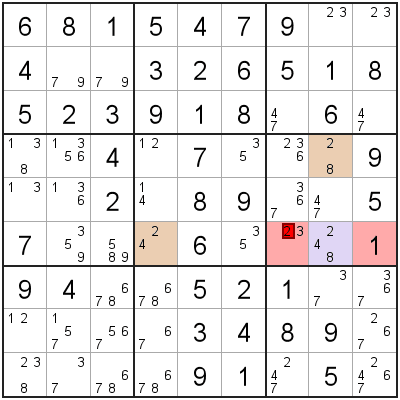
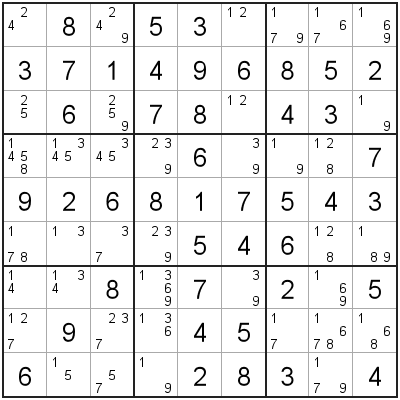
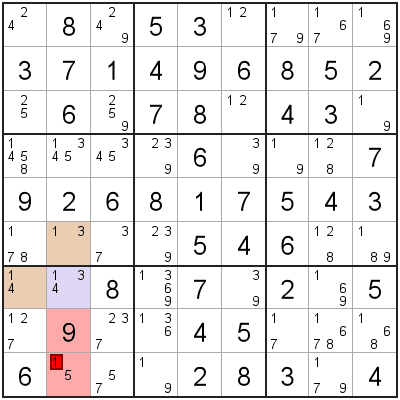
2 'Wing' cells (A, B) that have two candidates each, and have exactly one shared candidate.
A 'pivot' cell (C) that sees both 'Wing' cells, and has all three candidates (and no other candidates).

The three cells (A, B, C) making up the XYZ-Wing will have exactly one shared candidate ('1' in this example). We can remove this shared candidate from any cells that 'sees' all 3 XYZ-Wing cells.