How we make Fillomino puzzles

Fillomino puzzles aren't as popular as Sudoku puzzles, but they still give an interesting challenge! Each cell in a Fillomino puzzle has a number, and that number tells you how many cells are in that 'group'. Cells in a group may be linked horizontally or vertically, but not diagonally.

Here is a Fillomino starting grid,

and the finished grid,

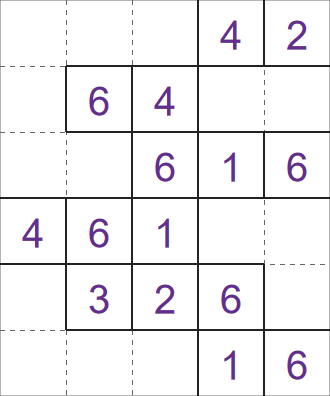
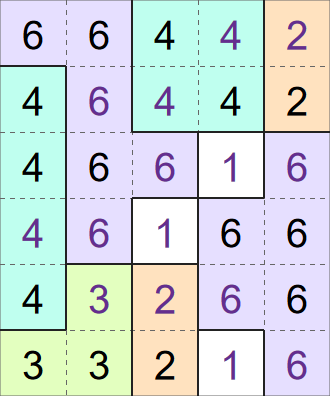
Fillomino solver

It doesn't matter what kind of puzzle we are looking at making, the process always starts with us working out how to solve those puzzles first. Once we have worked out the techniques involved, we can codify those techniques in to an algorithm, and produce our solver.

There are three steps we take to solve a Fillomino puzzle:

We first look for groups that only have one option for expansion. Take a look at the '6' in the bottom right of the example puzzle above. We know this group requires 6 cells, and the only option for expansion this group is to expand upwards.

We can apply this technique for lone cells as in the example above, and we can also equally apply this technique for when we have 5 out of the 6 required cells, for example. If there is only one expansion option, then the group must expand in that direction.
Our second step is to look for cells where only one group can reach that cell. Take a look at the partially completed grid below,

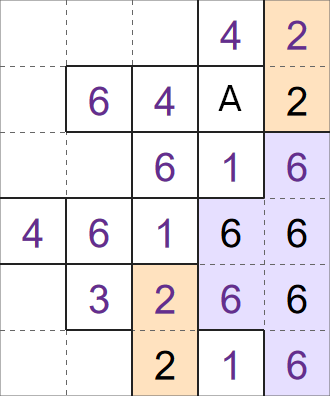
Look in particular for the cell labelled 'A' in the grid above. The '2' group already has the required number of cells, so that group can't expand in to cell 'A'. The only group that can expand in to cell 'A' is the '4' group, so we can insert a '4' in cell 'A'.

It should be noted that this step isn't particularly exhaustive - we don't look in-depth at the path a group would need to take to reach a given cell. More on this topic in the next step.
The first two techniques above will completely solve small Fillomino puzzles, and will solve large portions of bigger puzzles. Consider the situation below,

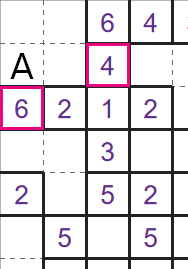
This is a portion of a bigger grid, and we are particularly interested in cell 'A'. In theory there are 2 groups that could expand in to this cell - the highlighted '4', or the highlighted '6'.

Step 2 above would look at these possibilities and decide that both the '4' and '6' group are valid options for cell 'A', and decide that no conclusion can be made about that cell yet.

This step looks a little more in detail and will notice that if cell 'A' was a '4', then this would mean the highlighted '6' group doesn't have enough space to expand in to, i.e. it would give us an invalid grid. This step would then conclude that cell 'A' must be a '6'.

This example is a little contrived in that steps 1 and 2 together looking at all the cells in this area would have solved this area without needing to reach step 3. Hopefully it illustrates the extra diligence that step 3 takes when looking at the possibilities for each cell.

The way our Fillomino solver (indeed, all of our solvers) works is that it will only move to step 2 when step 1 yields no progress. Likewise, it will only move to step 3 when step 2 yields no progress. This is because of the computational cost - step 1 is very cheap to execute, step 2 is a little more expensive, and step 3 is much more expensive from a computational cost point of view. This means our solver executes in the shortest time frame possible.

Fillomino generator

Now we have a solver, we can look at making Fillomino puzzles. These are the steps involved,

We start with a blank grid with no numbers inserted.
We pick a random cell, and look at it's neighbours. If it doesn't have any neighbours with existing groups, we will start a new a group and insert a '1' in this cell.

If any of the neighbours already have a group, we will pick a random neighbouring group, and extend that group to include this cell. We don't care at this point how many cells are in our chosen group, we just want to add this cell to an existing group when one exists.
We find that the second step might inadvertently create two groups of 5 cells (for example) right next to each other, i.e. this is really a super-group of 10 cells. Whenever we find this type of group we merge them together so that we have a completely filled grid where all the cell values accurately represent the group sizes.

It's very possible that this step will give us groups that are bigger than 9 cells. We don't worry about this for now.
We now break up all of our larger groups. This includes groups that are bigger than 9 cells. We also have a quota on the number of groups that can have 7, 8, or 9 cells - the exact quota depends on the total number of cells in the puzzle. There is no restriction on the number of groups with 1, 2, 3, 4, 5, or 6 cells.

When we find a group that is too big, we will remove those cells from the grid (i.e. insert a 0 for those cells).
We are (probably) now in a position where some of the grid is covered with inserted numbers, and some of the grid is blank. We go back to step 2 with the current state as our starting point and repeat the process until we reach this stage with a complete grid.

For bigger grids, this is likely to take a few iterations.
We now have our completed grid. The final step is to remove individual cells, and check to make sure our solver can solve the resulting puzzle. We will continue to remove values from cells until we can't remove any more values.

It's because of this step that we need to make sure our solver can complete in a reasonable time frame - this last step will run the solver on many grids before arriving at our final starting grid.

Conclusion

This gives us our starting Fillomino puzzle! Like many of our puzzles, the steps above look quite chaotic, and not particularly well planned. We always start out with a plan of how to make our puzzles. What we normally find is that our initial plan ends up producing puzzles that aren't interesting to solve, or are too easy, or too hard. We will modify our process to encourage or discourage the properties that we want, and the result is a process that looks 'grown' rather than planned!

This is a high-level overview of how we make our Fillomino puzzles, hope you found it interesting! Let us know if you have any questions, or if there is a particular step you would like to know more about!