How we make Network puzzles puzzles

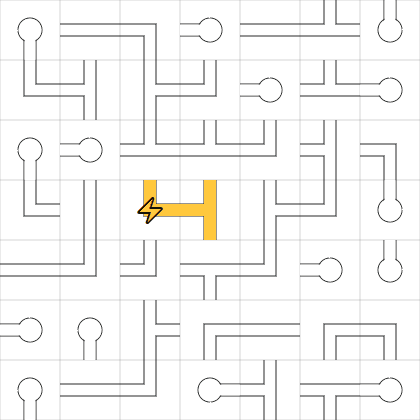
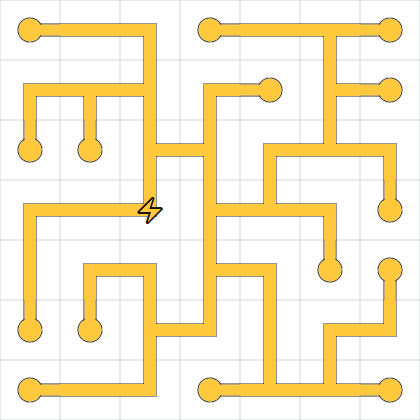
If you're not familiar Network puzzles, this is a starting puzzle,

and this is the solution to the above puzzle The aim of the puzzle is to rotate each piece so that every cell is connected (and lit up) by the power (⚡) cell. These puzzles are not as popular as Sudoku, but we like them, and think they are worth playing!

Network puzzle solver

As with every type of puzzle, we always start with a solver. We will always start by looking at how we, as human beings will solve a puzzle. We only resort to brute-force approaches when there is no alternative. We think this gives us puzzles that people will enjoy playing.

For Network puzzles, we have developed a notion of required 'connects', and available 'connects'. Take this portion of a Network puzzle:

None of these cells have been lit up yet, but that isn't the aim here - it doesn't really matter if a cell is lit or not. The real aim of a network puzzle is to arrange the pieces so that all the cells are one connected whole, and there is only one way to do that. The power cell and whether a cell has power or not just gives you a sense of progress.

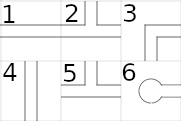
Let us suppose that we have already decided that cell 5 is in the correct orientation (doesn't matter how) - it doesn't have power (yet) and that's fine. If we now look at cell 4, cell 4 has a demand from cell 5 - cell 4 must 'connect' to cell 5, and that gives us only one orientation for cell 4, i.e. it must be in the horizontal orientation.

We can also look at cell 6 - cell 5 requires a 'connect' from cell 5, and there is only one way that this requirement can be satisfied..

We can look at cell 2 - cell 5 requires a connect from cell 2, but we don't have enough information to decide on an orientation for cell 2. Both cells 1 and 3 can be rotated so that they are available to connect to cell 2. In this situation we can say that cell 5 requires a connect from cell 2, and cells 1 and 3 are available for connect from cell 2. We don't know anything about the cell above cell 2 - this is only a portion of the puzzle.

If you look at the solving techniques on our Network page, you will see that the help on the page talks about looking at straight and T-shaped pieces around the edges first, and then moves from there. We can still think about this in terms of 'connects' - a 'T' shaped piece on the edge of the puzzle has connects available in 3 directions, and also has a direction in which no connect is available, i.e. the outside of the puzzle. This gives one possible orientation for this piece - and this is true if a T piece is on the edge of the puzzle, or in the middle of a puzzle.

By using the idea of required and available 'connects', we have codified most of the solving techniques used for this type of puzzle, i.e. we have generalised on the concept.

This technique allows us to solve most of any single Network puzzle. As is quite common with puzzles of this type, the last few cells can't always be found using this technique. In this situation a human player will either just look at a puzzle and be able to see a solution, or will discover the solution from semi-randomly turning the cells until they can just 'see' the solution.

This is always problematic to implement for an algorithm-based solver, you can't write software that can intuitively just 'see' something like that. In this instance, we resort to some kind of backtracking algorithm for the remaining cells. We will only do this when there is a small number of cells remaining. This makes sure that we don't end up with a puzzle that a computer can solve, but a human player cannot.

When thinking in terms of required and available 'connects', we are guaranteed this will only find a unique solution. When implementing a backtracking algorithm, we will always make sure to implement it to check for all possible permutations - we don't want to present a solution that may not be unique. We are only interested in puzzles with unique solutions, so we need to make sure our solver behaves in this way too.

Network puzzle generator

The generator is much simpler in comparison. We start from a blank grid, and go through these steps,

1. Pick three random cells that are next to each other. There are only two orientations for this,
   • They are all in a straight line, in which case we can link them with a horizontal or vertical pipe (| or - piece), and two end node pieces.
   • They are in a L-shape, in which case we can link them with a L-piece, and two end node pieces.
2. We will say that a cell is expandable if another cell can be joined on to it. An end-node is expandable because we can join another cell on to it by turning it in to a straight piece, or a 'L' shape piece.
   If we have a straight piece, or a 'L' shape piece we can add another cell by turning it in to a 'T' shape.
   A cell with a 'T' shape is not expandable, as we can't add another node to give us a cross-shaped piece - those are not allowed under the rules.
   We will create a list of all the undecided cells next to expandable cells, and choose one at random. We will extend the network in to that cell.
3. We will now repeat step 2 as many times is required until the entire puzzle is filled. If it is not possible to extend the puzzle in this way, an empty cell may be surrounded by T-cells, for example, then we will throw this layout away and start again.
4. We will now reset all of the cell orientations to 'unknown', and give the grid to our solver. If our solver can solve it, and decides it only has one unique solution, then we have our puzzle!

This is a high-level overview of how we make our Network puzzles. We hope you find this interesting, please contact us if you have any questions about this approach!