How we make our Sudoku puzzles

We sometimes get questions around how we make our Sudoku puzzles, and what the difference is between an easy and a medium puzzle, for example.

All of our puzzles are generated by a computer program - I've lost count of how many puzzles we publish each day, but it's in the region of 100 puzzles a day. It would be very time consuming to make that many puzzles by hand for every single day!

Having said that, we want to make puzzles that actual people enjoy solving. There is a difference between hand-made puzzles and puzzles made by a computer, but I believe our approach to making puzzles makes that difference as small as possible.

The Sudoku solver

It doesn't matter what kind of puzzle you are looking at making, everything starts with the solver.

In my experience, this is the evolution of a (human) Sudoku player,

• When you first discover Sudoku puzzles, you spend your time looking randomly at the rows and columns for a number to insert. You're not particularly methodical in your approach, you scan the puzzle hoping that you happen to see a number you can insert.
• You can continue with this approach for medium puzzles, but you will need to start becoming more methodical. You will start scanning the rows and columns in order for example. You may not be methodical all of the time, it may come and go, but there will be some methodical element in there. You may use pencil marks in some parts of the puzzle to help you.
• By the time you move on to hard puzzles, you will almost certainly be using pencil marks to help you. You may not use pencil marks everywhere, but their use will certainly be extensive.
• For the tough puzzles, the use of pencil marks will be widespread, and you'll be using the more advanced techniques such as naked pairs and box-line reduction.

Now that we've worked out what differentiates a human player that enjoys easy puzzles from a player that enjoys medium puzzles (for example), we can work on our solver.

The truth is that a computer can't look randomly at a Sudoku grid looking for a number to insert. The first thing the computer will do is to generate pencil marks for this whole grid. We can however do different things with those pencil marks for different difficulty levels,

Easy: For easy puzzles we will look at each row, column and 3x3 region to see if there is only place we can insert each number. For example, we know that every column has to contain the number '5', we will look to see if there is only one place we can insert a '5'.

Medium: In addition to the easy techniques, we will also look to see if each cell has only one candidate. We might look at a particular cell, and decide by a process of elimination that the only number we can insert is a '6', for example. This is very similar to the easy technique, but novice Sudoku players don't normally do this, in my experience. For medium puzzles we place some restrictions on how many cells in a column are already filled, and won't apply this technique if there are too many empty cells.

Hard: We apply the same techniques as for Medium puzzles, but with no restriction on how many empty cells are in a given row/column.

Tough: It is only at this difficulty we start using the advanced techniques.

Having a solver now means we can grade a Sudoku puzzle - if a Sudoku puzzle can only be solved using the Easy techniques, then it's an easy puzzle! If a Sudoku puzzle requires us to use the hard techniques, but not the tough techniques, then it is a hard puzzle.

There are quicker ways for a computer to solve a Sudoku puzzle. There is plenty of (sometimes academic) literature available that will talk about backtracking algorithms, branching, and difficulty scores, and that's great if your aim is to simply write a Sudoku solver. This approach will give you a difficulty score, but it tells you how difficult it is for a computer to solve a puzzle, and not how difficult it is for a human player to solve a puzzle.

The Sudoku generator

Now that we have a Sudoku solver, we can start looking at a Sudoku generator. There are two steps to generate a Sudoku,

1. Generate a completed Sudoku grid
2. Remove values until we have a suitable starting grid

Let's look at both of these in turn,

Generate a completed Sudoku grid

The first part of generating a Sudoku is to generate a completed grid, and there are many valid ways to do this. We use a classic backtracking algorithm. We start with an empty grid, and fill the grid with pencil marks, so that it looks like this,

Our backtracking algorithm starts with the cell in the top-left, going through these steps,

• We put the pencil marks for that cell in to a random order.
• We take the first pencil mark, and insert that value in to the cell.
• We now run the grid through the Hard solver. The hard solver runs very quickly, and we can afford to do this on every step. For the first cell, the solver isn't going to be able to make a great deal of progress. In fact, the only thing it will do is reduce the number of pencil marks in some of the cells.
• We move on to the next cell and repeat the process.
• At some point, we will probably reach a cell that doesn't have any pencil marks in it, i.e. the grid is impossible at this point. When this happens, we will go back to the previous cell, and try a different value. If we try all of the different values for the previous cells, but we still can't fill this grid, we will go to the previous cell before that, i.e. the classic backtracking algorithm

This approach will eventually give us a completed Sudoku grid, and this will be the solution to our Sudoku puzzle.

Remove values until we have a suitable starting grid

Before we start this stage, we will need to know what difficulty Sudoku we want to generate. Let's assume we want to make a Sudoku of Medium difficulty. The steps we need to go through are,

1. Put all of our cells in a list, and randomise order.
2. Take the first cell from our list, and remove the value from the grid.
3. Take a copy of the Sudoku we have, and give it to our solver, i.e. in this example, can our medium difficulty solver finish this puzzle?
4. If our solver can finish this puzzle, we go back to step 1, and move on to the next cell from our list. It's important here that our solver is running at the difficulty we need. Our solver running on the 'hard' setting might be able to solve a puzzle, but if we want to make a medium puzzle, it needs to be solvable on the 'medium' setting.
5. If our solver can't finish this puzzle, we put the value back, and move on to the next cell.

When we have finished going through all the cells in the grid, we have our starting Sudoku grid! We know that it won't be any harder than our desired difficulty, but it could be easier. As a last step, we trying solving our Sudoku at the next easiest difficulty.

In this example, we want to make a Medium difficulty puzzle. We want to make sure our solver running on the 'easy' setting isn't able to solve it. This gives us our starting Sudoku grid!

What about other variants of Sudoku?

We have over 10 Sudoku variants, but the steps we take are the same. The only thing that changes between the different variants is how we create the pencil marks for each step. Take this example of a X-Sudoku grid,

We have applied the standard set of Sudoku rules to insert the pencil marks for this grid, but we can go further and remove some of the pencil marks on the diagonals as well. Once we have done this, the next steps to solve this X-Sudoku are the same as for a standard Sudoku puzzle, i.e. we look for single candidates, etc.

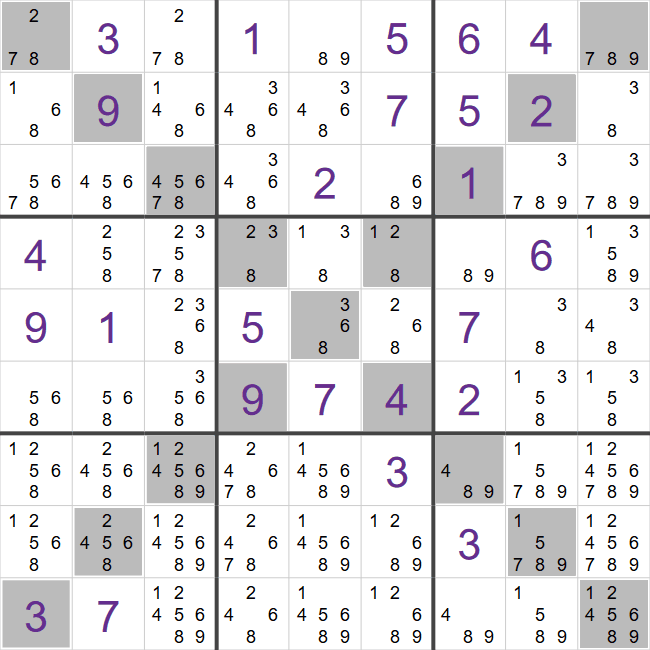
We can apply this technique for any Sudoku variant. For 12x12 and 16x16 grids, we have more cells, but the overall process is the same. For Arrow Sudoku puzzles, we have a more complex set of constraints, but we take the same steps, i.e. we insert the pencil marks as if it were a standard Sudoku, and then methodically analyse each 'arrow' and only keep those combinations of pencil marks that satisfy the total for that arrow.

What is your Sudoku generator written in?

Our Sudoku solver is written in C++. There are a few reasons for this, but the main reason is that C++ was the language I was most proficient in at that time. I could claim that C/C++ will be faster than a higher level language such as Python, or javascript, or similar. My experience is, your running times will depend much more on algorithm design, than choice of programming language.

A reason I continue to use C++ is that I am confident that C++ will still be continued to be supported in the future. I created puzzlemadness in 2009, which at the time of writing was 11 years ago. I use the current version of Visual Studio to compile my puzzle generator, and I've not had to make any changes to my codebase to accommodate newer versions of compilers/libraries in that time. I can be confident that my codebase will continue to compile and run without modification in another 11 years. I'm not sure I can be confident of that in some of the other languages that are available today.

The computer I currently use has 4 CPU cores. To take advantage of this, my puzzle generator is multi-threaded, and is configured to use 3 threads, i.e. 3 CPU cores. This leaves 1 CPU core available, which is plenty for most other tasks I want to perform. This means that I can generate puzzles and do something else at the same time.