How we make Suko puzzles

Suko puzzles are a little different to most of our puzzles in that they are so small. Compare a Suko puzzle to a standard Sudoku puzzle, a Sudoku has 81 cells compared to only 9 cells for a Suko. This made it very tricky to find a way to differentiate between an Easy, Medium and Hard puzzle.

We don't need to have three different difficulties for every type of puzzle, but we believe it is one of the things that separates us from every other puzzle site out there. During most of the development we thought we would only be able to find a way to have easy and hard Suko puzzles - based solely on layout. We did eventually find a way to make medium puzzles.

This is an example of a Suko puzzle:

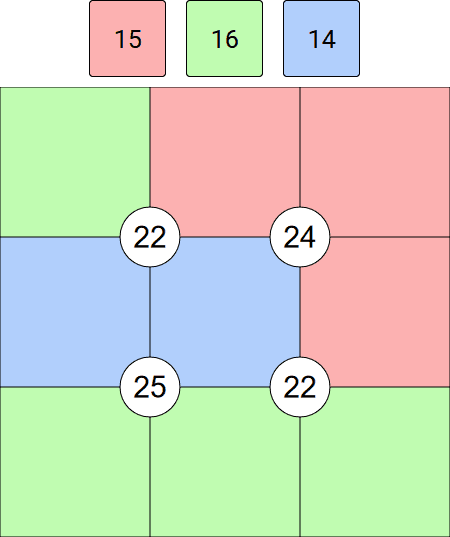
We will call the totals in the grid the quadrant totals, and we will call the totals given at the top of the puzzle the layout totals.

Suko solver

Everything start with the solver, and Suko is no different! These are the steps our solver will go through to solve a Suko,

1. We use pencil marks on Suko puzzles. The first step is to set all the pencil marks for every cell on, i.e. each cell will have the pencil marks 1-9.
2. We use the quadrant and layout totals to refine the pencil marks. If a number in a given cell means we can't meet the quadrant or layout total requirements, then we will remove that pencil mark from that cell. We will carry out this step fully aware of any numbers that are already inserted in any cells.

3. We will look at the nature of the overlaps between quadrant and layout totals. We can extract extra information from these overlaps. From the example grid above, we can see that the reddish cells are completely within the top-right quadrant, this actually means we can deduce what the center cell is.

   Similarly, the blue cells are completely contained within the top-left (and the bottom-left) quadrant, this means we can deduce that the top-left, and center-left cells must total 8 (22-14). In this example, this has a significant impact on the pencil marks in those two cells.

4. We now look for pencil marks that only appear once in the grid, and for cells that only have one pencil mark. After this step, we normally return back to step 2 to run through the process again.

5. At this point, if we're not able to make any further progress, we will resort to using a backtracking algorithm. All of the steps up to now are in essence how you or I might solve a Suko grid - they have to be adapted slightly so that they can be codified in to a set of algorithms, but the fundamental ideas are the same.

   Taking a backtracking approach means trying every combination of numbers, until we find the solution. We start in the top-left cell and work our way across to the right, and then on to the second row. By the time we reach this point we will definitely have some pencil marks in every cell, and we might also have some numbers inserted in to some cells. We will only try those numbers that appear as pencil marks for each cell, i.e. if a cell has pencil marks '3' and '5', we will only try those in that cell when backtracking. A naive approach might try every number from 1 to 9.

   Our solver is only interested in Suko puzzles that have a unique solution. If the backtracking portion of this solver finds multiple solutions for a particular puzzle, then it will report that it wasn't able to solve this puzzle.

Suko generator

Compared to many of our puzzles, the Suko generator is quite simple. Here are the steps,

1. Generate a layout. The layout of a Suko puzzle plays a big part in how easy or difficult that puzzle will be.

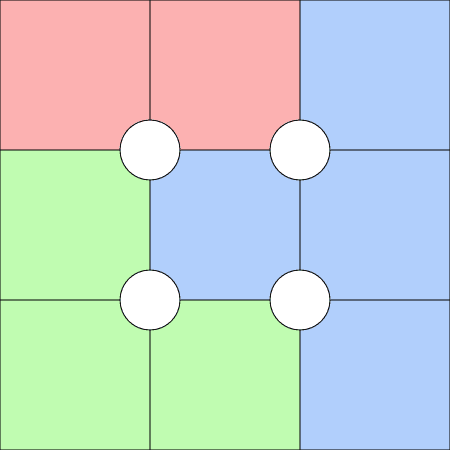
   This is an example of an easy layout:

   

   And this is an example of a hard layout:

   

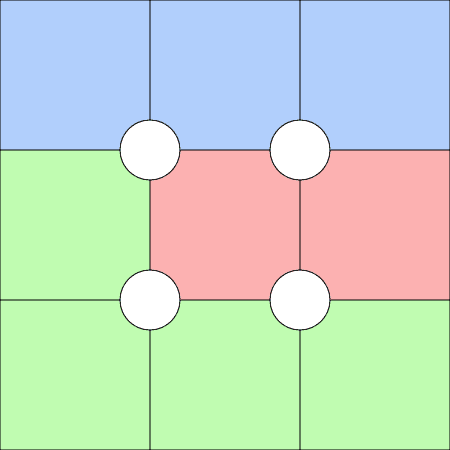
   Note that for the easy layout we are always going to be able to insert one, probably two numbers straight away without needing to work too hard. Whereas for the hard layout, we need to look in depth at the pencil marks for each cell.

2. Insert numbers in to the grid, and calculate the layout and quadrant totals. For some puzzle types, this step can be quite tricky, but this is really straightforward for Suko puzzles.
3. Solve the puzzle to make sure it has a unqiue solution.

As I mentioned earlier, it was a little tricky to find a way to differentiate between easy, medium and hard Suko puzzles. This is how we do it,

• Easy: Easy layout, and requires no backtracking to solve.
• Medium: Easy layout, and does require backtracking to solve.
• Hard: Hard layout, and does require backtracking to solve.

Conclusion

That explains how we make and grade our Suko puzzles. They are one of the smallest puzzles we make, but they provide plenty of challenge!

We hope you found this interesting! Let us know if you have any questions, or if there is a particular step you would like to know more about!