How we make Train Track puzzles puzzles

If you're not familiar TrainTracks puzzles, this is a starting puzzle,

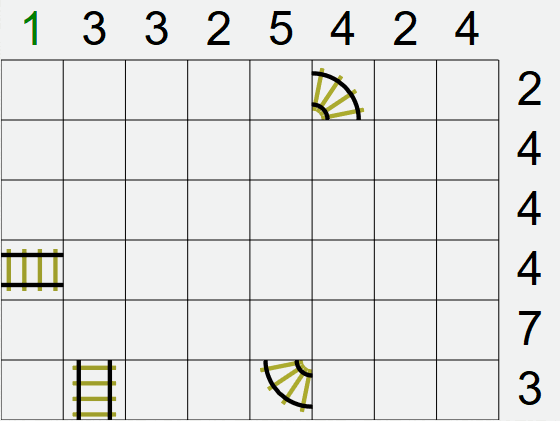
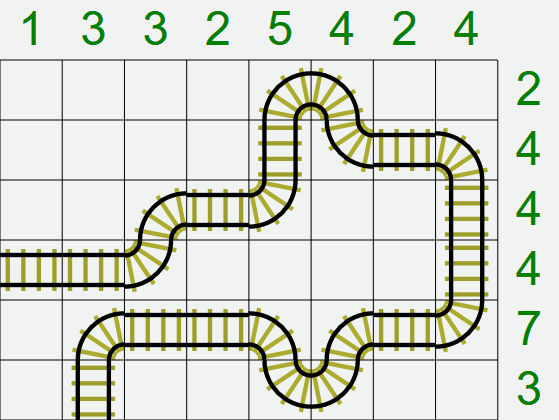
Train Tracks solver

We always start with a solver. We try to make our solver so that it solves puzzles in the same way as a human solver would do. We will solve many train tracks puzzles from different sources, work out how we solve them, and try to write that down as the basis for an algorithm. Train Tracks is no exception!

These are the steps we take to solve a Train Tracks puzzle,

1. Look for completed rows and columns. If we find a completed row/column, we will insert a 'X' for all other empty cells in that row/column.
2. We insert a '?' for any cells implied by existing tracks. Each track piece has two entrances/exits pointing at two cells. We may not know exactly what track type to insert in to those two entrance/exit cells, but we do know that there will be a piece of track there, so we insert a '?' as placeholder for those cells.
3. We insert a '?' for any cells implied by the clues. For each row/column we will count the number of empty cells, and subtract that from the length of that row/column. If this number matches the clue for that row/column, we can insert a placeholder '?' for all empty cells.
   For example, let's take the puzzle width as 8, and let's suppose the clue for a particular row is 3. If there is already 5 empty cells in that row, we know the remaining 3 must contain track pieces.
4. Fill in dead ends. In this context, this is an example of a dead-end:
   There is no way that a section of track can enter this dead-end and emerge somewhere, so we can mark all of these cells as empty.
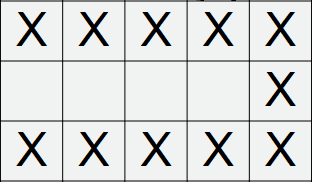
5. Fill in implied track pieces. We look for any cells that have 2 track entrances/exits already, and fill those in. This is an example from the middle of a grid,
   There is one empty cell left in this part of the grid. We have two sections of track 'pointing' at this cell. It doesn't matter what else is around this cell, we know which type of track to insert here.
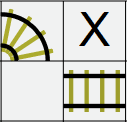
6. Bifurcate. The steps above will solve most puzzles. For those puzzles that are still left unsolved, we need to resort to essentially 'guessing'. We look for implied cells that have only two possibilities, and try them both. This means inserting a section of track, and running our solver on the grid. If this gives us a grid that is not valid, i.e. a contradiction, then we know that this was the wrong track piece to insert.
   We don't like taking this 'brute force' approach to solving any type of puzzle, but sometimes it is the only sensible option. With Train tracks puzzles, we normally find we only need to use this technique at the end of a puzzle. In this situation somebody solving a puzzle will be able to just 'see' the solution, without needing to use any particular solving technique. With this in mind, we only apply this technique when there is a limited number of cells left to fill. This makes sure our puzzles are satisfying to solve, and somebody solving our puzzles doesn't need to 'guess' at any point.

Making Train Tracks puzzles

The solver is always the starting point for any type of puzzle - without a solver you won't be able to write a generator. This is the steps we go through to generate a Train tracks puzzle,

1. Make the finished grid. We make a random path across the grid, starting at a cell on the puzzle boundary. We have a minimum target 'coverage', i.e. the minimum number of cells we want to be in our path. If we have reached the target coverage, and are on the puzzle boundary, we will call this our exit. If our path hits a dead-end and can't move forward any further, we start again from a blank grid.
2. Make the clues. We count the number of pieces of train tracks in each row/column, and set that to be the clue for that row/column. If we find any rows/columns that have no sections of tracks, we throw that puzzle away, and start again at step 1.
3. Remove sections of track. We randomly visit each section of track, remove that track section, and see if we can solve this grid. We will continue to remove sections of track until we have tried all sections (apart from the start and end sections).

This process gives us our puzzle! It might seem that steps 1 and 2 are quite wasteful in that we will end up discarding many puzzles. This is true, but bear in mind that the most expensive step in terms of computation time (by a long way) is the final step. This means it's not as wasteful as it might seem at first glance.

This is a high-level overview of how we make our Train tracks puzzles, hope you found it interesting! Let us know if you have any questions, or if there is a particular step you would like to know more about!