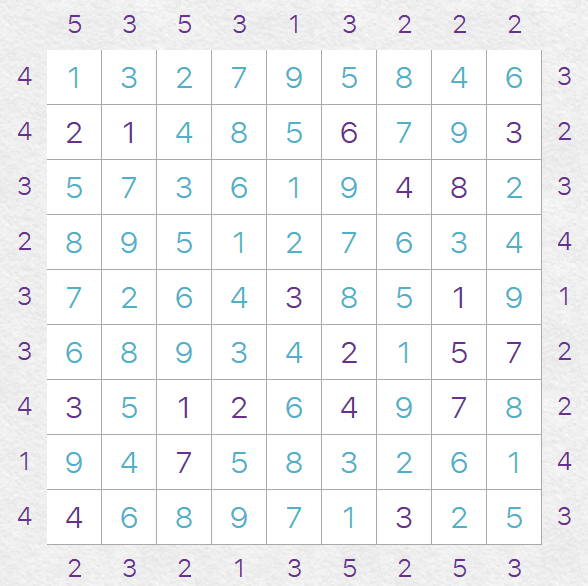
This is an example of a finished Towers puzzle. This puzzle borrows heavily from Sudoku puzzles, but
also has some of it's own rules. Firstly, this is a 9x9 grid, so each row and column must contain the
number 1-9 once and only once. If you have a 5x5 grid, then each row/column would have to contain
the numbers 1-5.
A Towers puzzle also has clues on both sides, and top/bottom. The clues tell you how many 'towers' you can
see if you were look from that point in to the puzzle. The number in each cell tells you the height
of that tower. As an example, take the top row looking from the left, we have a clue of '4'. Looking in
to the puzzle from that point we would see 1, 3, 7, 9 (i.e. four numbers/towers). The 2, 5, 8, 4, 6
would be hidden behind the higher numbers/towers before.
Take the left-most column from the top, we have to clue '5'. So, looking down that column we would be able
to see 1, 2, 5, 8, 9 (i.e. 5 numbers/towers). The 7, 6, 3 and 4 would be obscured behind the higher
numbers/towers before.
 Towers leaderboard
Towers leaderboard