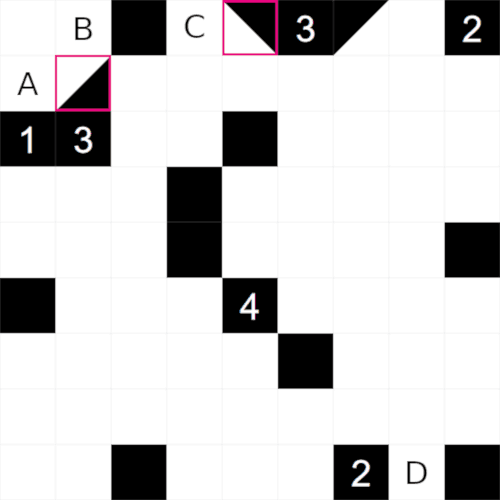
This is an example of a starting Shakashaka grid. The starting grid is mainly white, but with a small
number of black cells. Some of the black cells have clues, this tells us how many triangles surround
that cell.
I have highlighted two cells with a '3' clue. Let's look at the '3' clue on the right first. It tells us
that there are 3 triangles surrounding this clue, and with only 3 available cells, we know that cells
'D', 'E' and 'F' must all contain triangles. We have 4 different types of triangles to choose from, but if we
look at cell 'D' first, we can see that the only triangle that can fit here is a top-right triangle.
Similarly for cell 'F', this cell must contain a top-left triangle.
Looking at the other '3' clue we are in a similar situation, we know that cells 'A', 'B' and 'C' must
all contain triangles. The easiest cell to look at is cell 'A', where the only valid option is a
bottom-right triangle.
 Shakashaka leaderboard
Shakashaka leaderboard