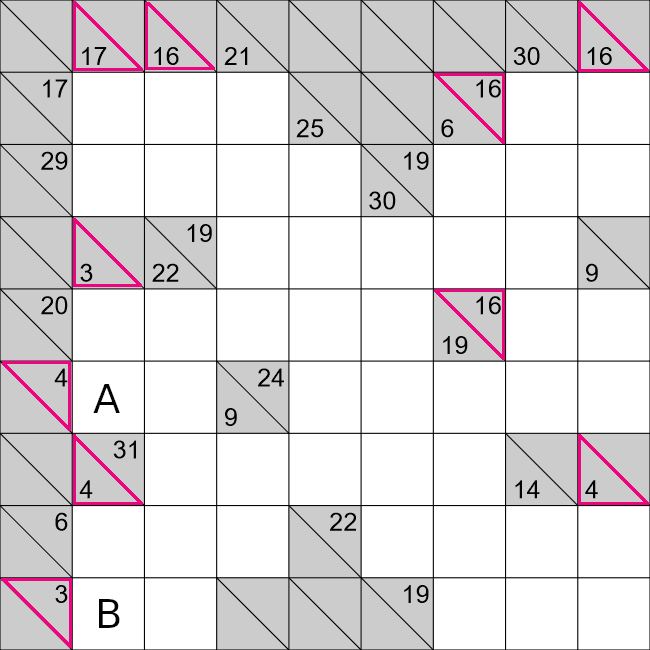
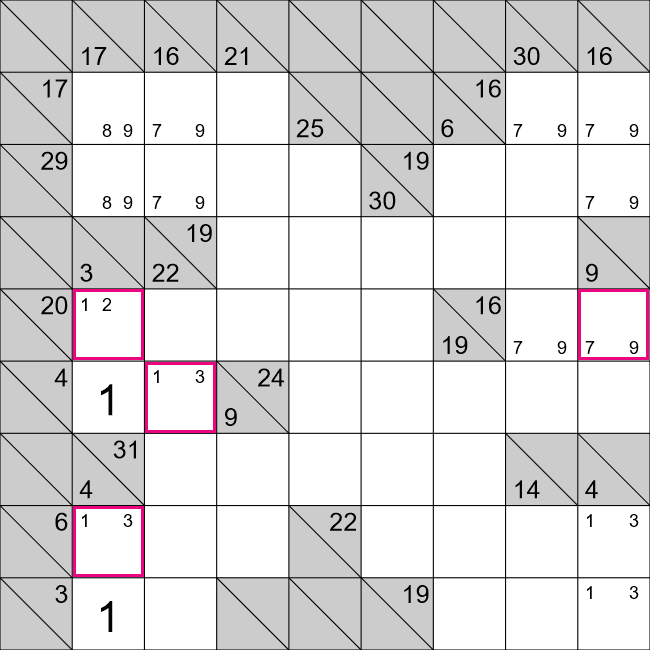
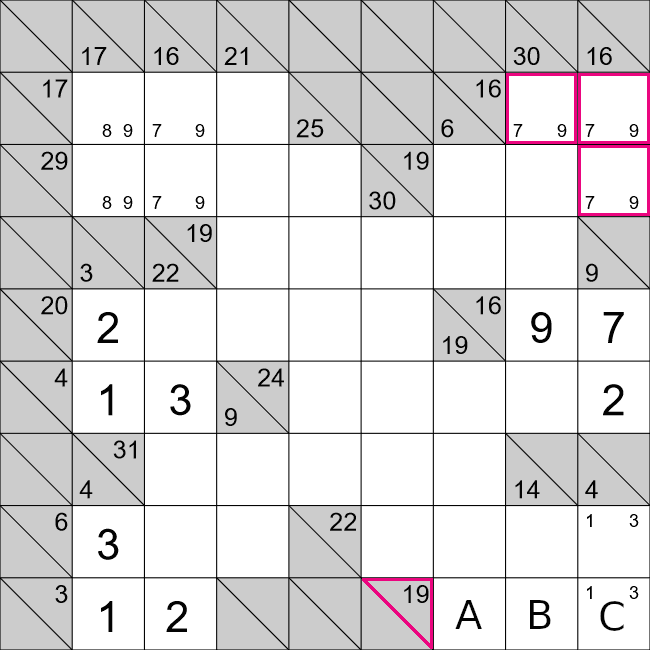
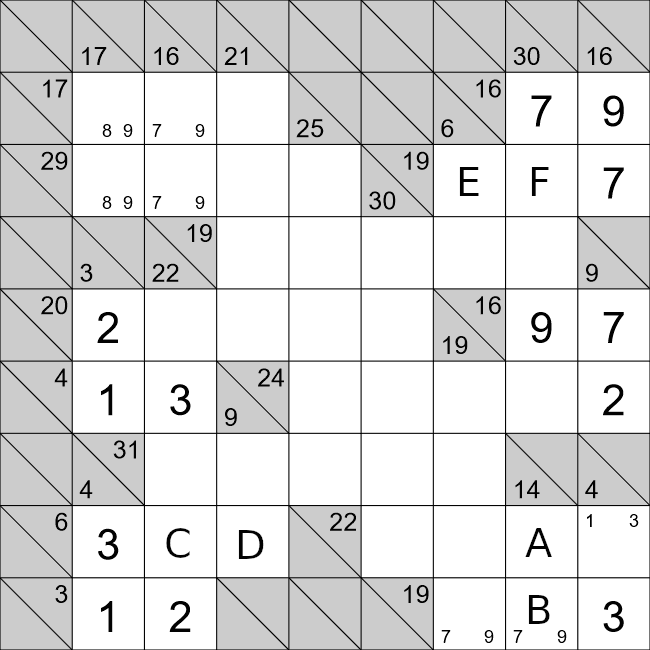
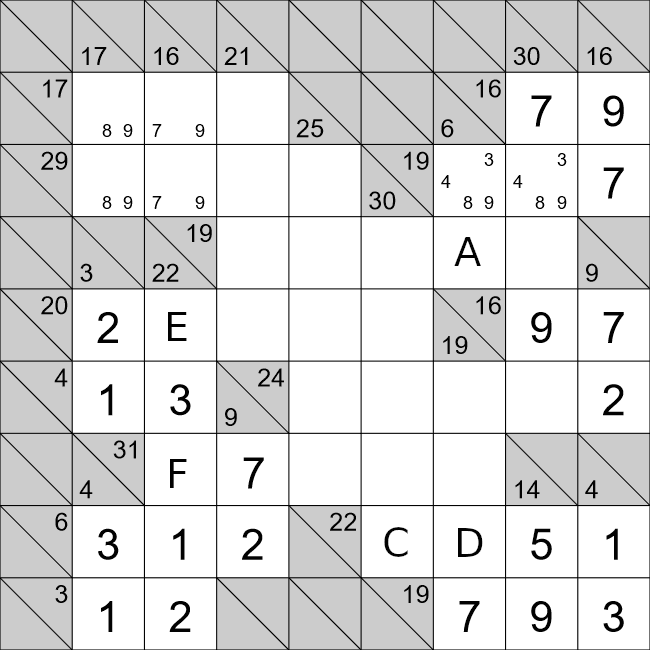
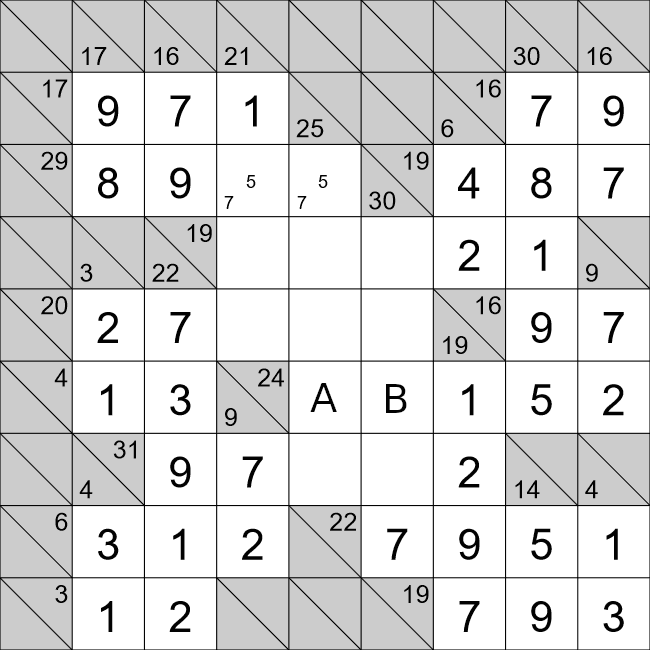
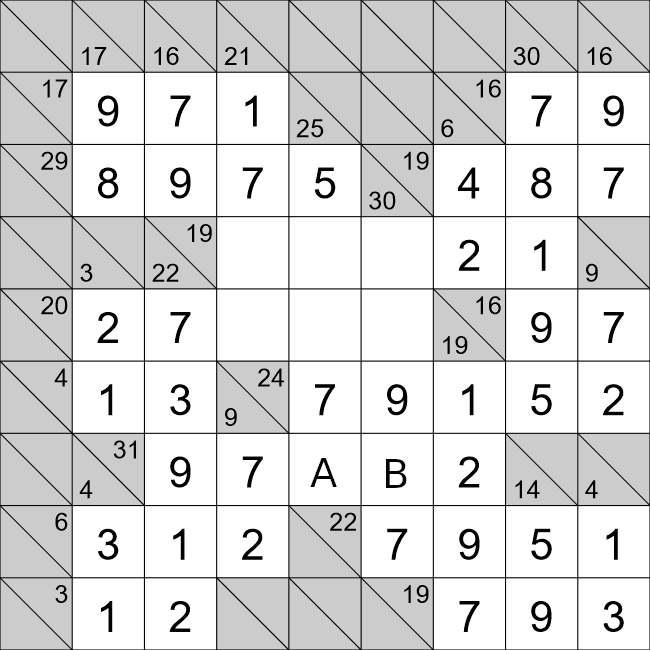
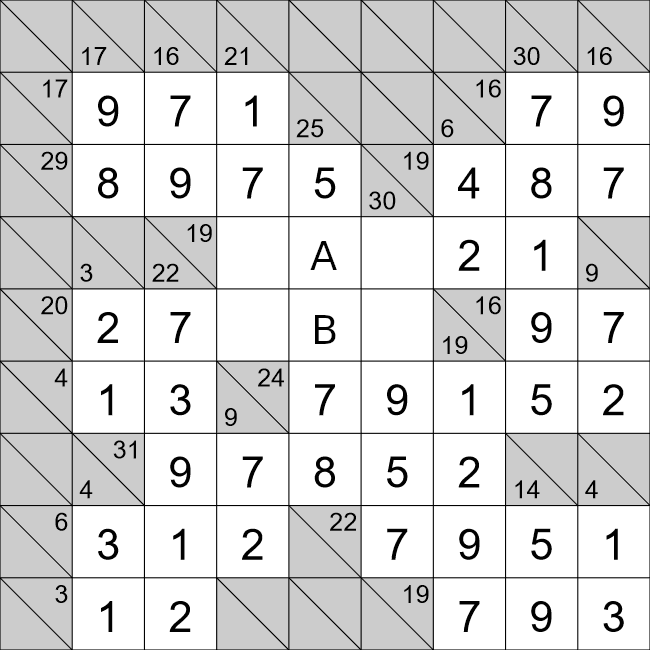
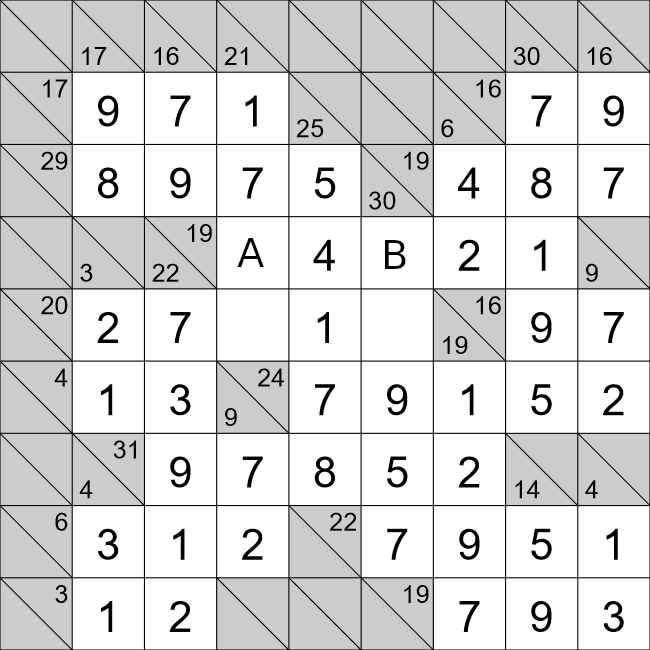
We will now look at cells A and B. For this horizontal row we have,
31=9+7+A+B+2
13=A+B.
There are a few ways we can achieve this,
- 13 = 9 + 4 ❌
- 13 = 8 + 5 ✔
- 13 = 7 + 6 ❌
The first and third options are possible because we already have a 9 and 7 in that horizontal run of
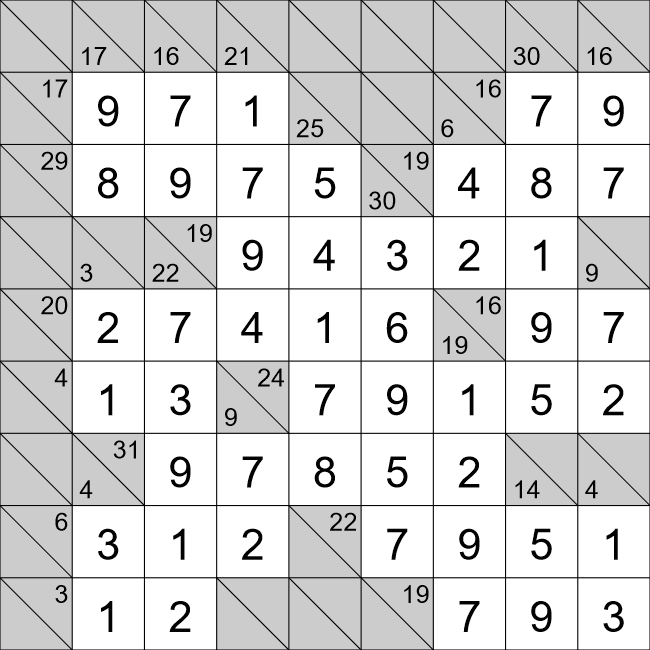
cells. That only leaves the second option. Cell A already has a 5 in that vertical run of cells, so cell
A must 8, and cell B must be 5.
 Kakuro leaderboard
Kakuro leaderboard