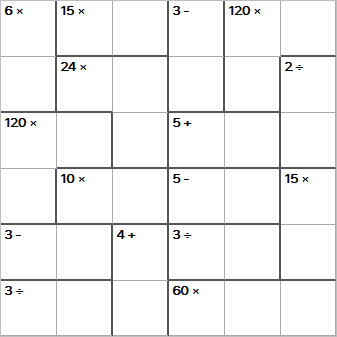
Daily Medium Mathdoku Puzzle for Thursday 21st November 2024

How to play

The rules of Mathdoku are based on the rules of Sudoku. This is an example Mathdoku starting grid.

A completed Mathdoku grid is like a Sudoku in that each row and column must contain the numbers 1-6 once and only once (notice that this grid is smaller than the standard Sudoku grid).

In addition, the grid is split up in to multiple sections, typically between two and four cells. Each section has a number and a Mathematical symbol. You must make that number by combining the numbers with the mathematical symbol.

This is the same grid as above, but completed. You can see that by combining the numbers with the mathematical symbol, you arrive at the target number.

As an example, the top-left block has two cells with the clue '6x', so this means you need to make 6 by multiplying the two numbers, and 2x3 does make 6!

With + and x, it doesn't matter which way round your numbers go. However, with ÷ and -, the order does matter. For Mathdoku puzzles, you can choose which way round the numbers go. So, in the bottom left we have the clues '3 -' and '3 ÷', it doesn't matter which way round the two numbers go in the cells. (It does of course matter for the general 'Sudoku' rule that each row/column must contain each number once and only once).

This is another example starting grid. We can't fill any numbers in immediately, and this is always the case with Mathdoku puzzles.

The first step with a Mathdoku puzzle is always to enter pencil marks for those cells that don't have many combinations. For example, the top-left cell with the clue '5x' is a great example. There is only way to satisfy that clue, i.e. 1x5 = 5. So we can enter 1 and 5 for the pencil marks for those two cells.

There are two ways to satisfy '6x', namely 1x6 = 6, and 2x3 = 6, so it's not worth looking at that block.

We have now entered some of the pencil marks, and we will use the 'naked pairs' technique here. For the column on the far-left, we have a pair of cells with the clue '20x', and we have the possibilities of 4 and 5. The 4 and 5 in this column must go in those two cells, we don't know which way round yet, but they must go in those two cells.

This means the top-left cell can't be a 5, and therefore must be a 1.

There are a further 3 cells we can now fill in, and this is quite often the case with Mathdoku puzzles.

Having filled this in, we can now look at the two cells in the top row with '7+' as the clue. We can't use 1, 5 or 6 again in this top row, so we can only make '7+' with 3+4, which means the last cell in this row must be a 2.

We have now made good progress in solving this Mathdoku, and you have just learnt the rules you need to be able to solve a Mathdoku puzzle.

You should now be able to work out the value that goes in the highlighted cell.

This page will automatically load the Mathdoku puzzle for today. If you want to play a different puzzle, go to the archive page and choose your puzzle.
There are two ways to play a Sudoku puzzle, you can just use the mouse/touchscreen, or you can use the mouse and keyboard. You can switch between the two methods any time you like, and can use a combination of both.

Playing with a mouse/touchscreen.

When you have found a square where you can enter a number, click/touch that square. The square will turn light blue.
Above and below the puzzle is the number selection. Click/touch the number you want to enter in to that cell. If there is already a number in that square, it will be over-written.
If you want to enter a pencil mark, click/touch the square you want to put in a pencil mark. It will turn light blue. Click/touch the pencil icon above or below the puzzle. This icon will turn light blue, and you are now in pencil marks mode.
Whenever you click/touch a number now, a pencil mark will be put in the square instead. To remove a number as a pencil mark, make sure you are in pencil marks mode, and click/touch the number again.
You can exit pencil mark mode by clicking/touching the pencil icon, it will turn back to normal.
If you want to clear a particular square, make sure that square is selected and is in light blue. Click/touch the eraser icon. If there is a number in that square, it will be removed. If you click/touch it again, any pencil marks in that square will be removed.

Playing with a mouse and keyboard.

You will need to select a square by clicking on it with the mouse, it will turn light blue. You can change the current square by using the cursor keys on your keyboard.
To enter a number, press that number on the keyboard. If there is already a number in that square, it will be overwritten. To remove a number, press the backspace or delete key on your keyboard.
To enter a pencil mark, press control, shift, or alt on your keyboard at the same time as pressing a number key. Do the same thing again to remove that pencil mark.

Any mistakes you make will be hilighted in red. The website will know when you have completed a puzzle and will tell you. If you have an account and are logged in, the website will remember that you have completed that puzzle. You will also take part in out leaderboards. It's free to create an account!

Daily Medium Mathdoku Puzzle

Thursday 21st November 2024

Mathdoku leaderboard

How to play

Playing with a mouse/touchscreen.

Playing with a mouse and keyboard.

Try our other puzzles!

Sudoku

Logic Puzzles

Card games

2 player games

Reset

Settings

Daily Medium Mathdoku Puzzle

Thursday 21st November 2024

Mathdoku leaderboard

How to play

Playing with a mouse/touchscreen.

Playing with a mouse and keyboard.

Try our other puzzles!

Sudoku

Logic Puzzles

Card games

2 player games