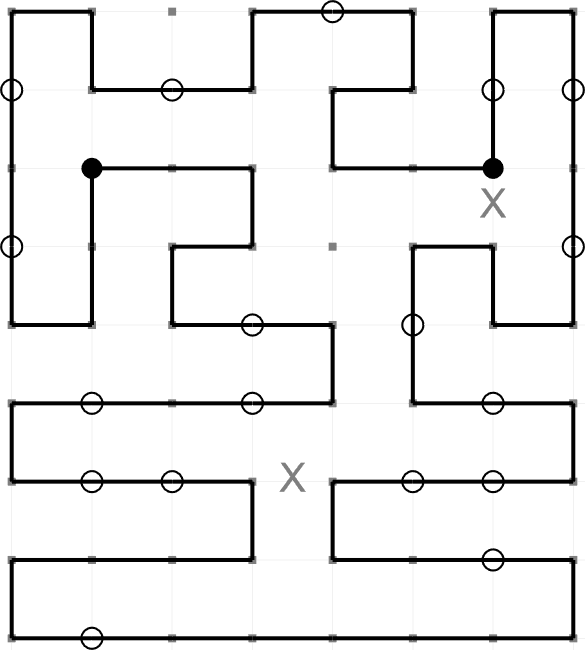
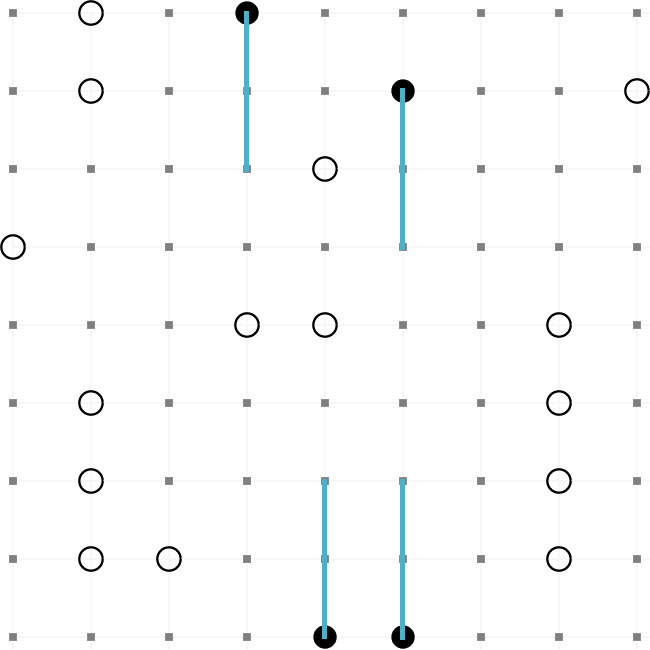
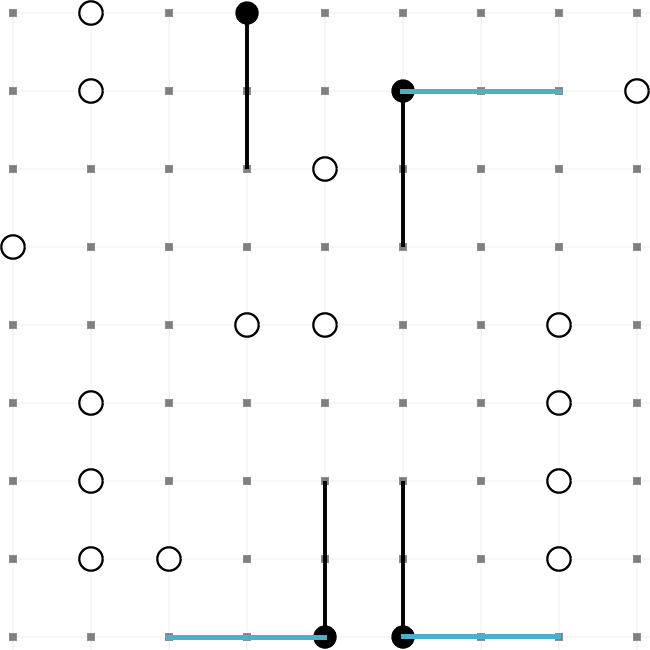
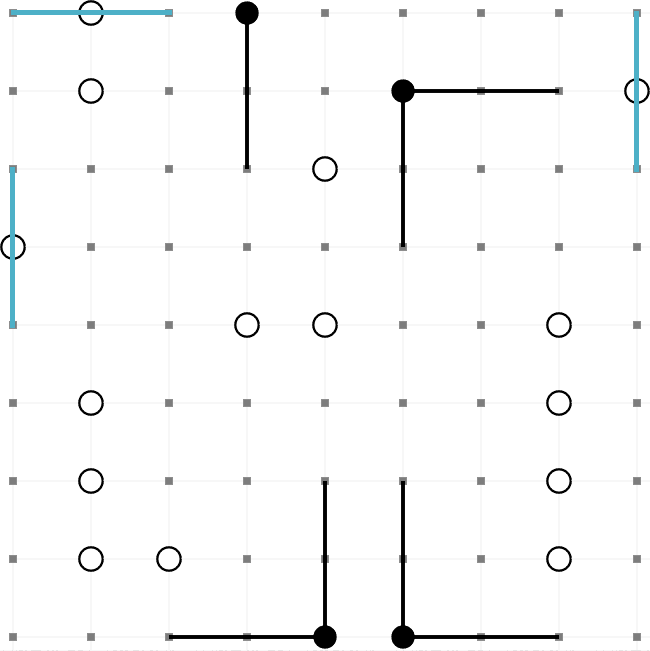
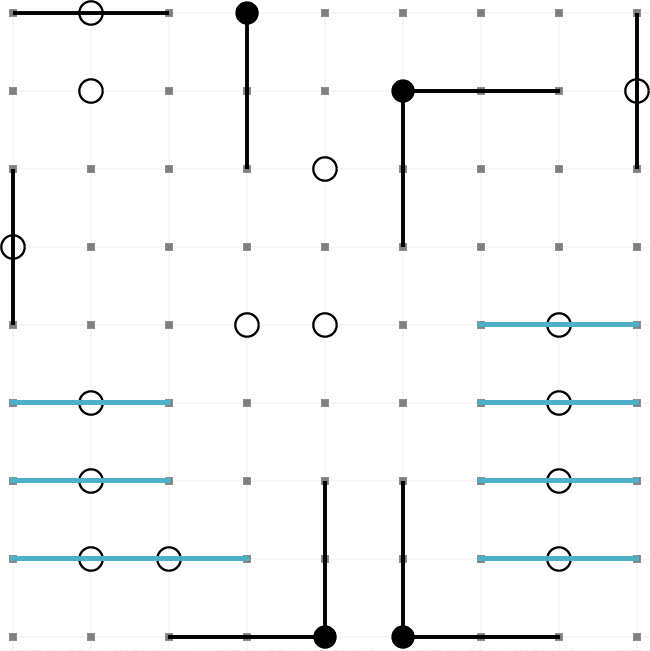
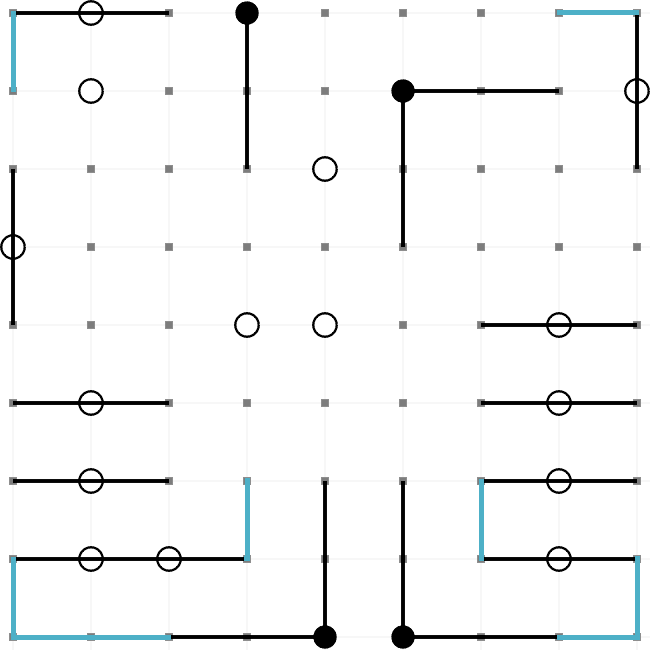
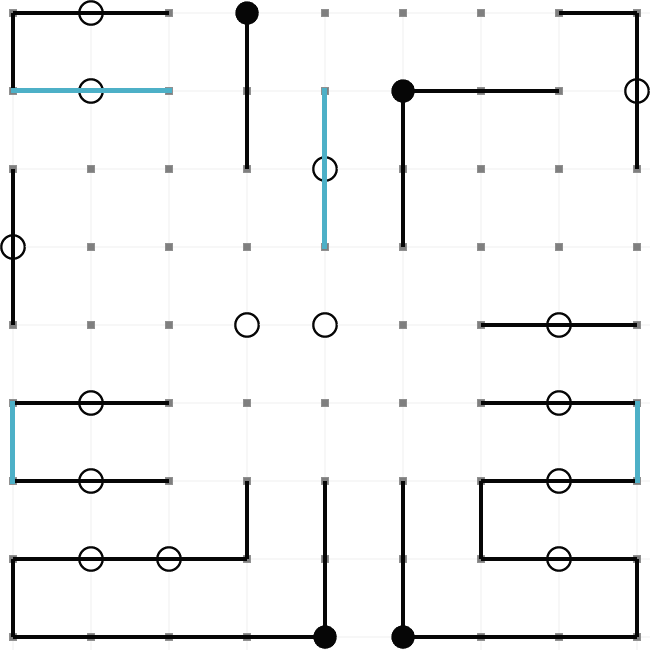
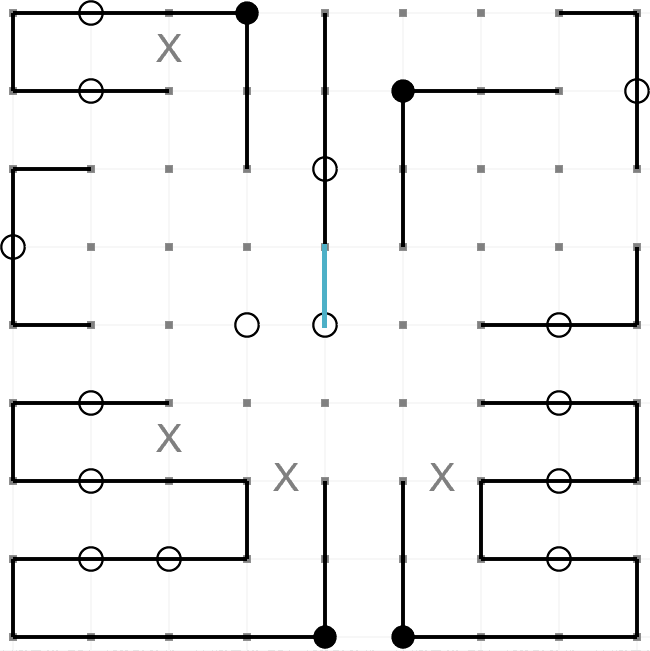
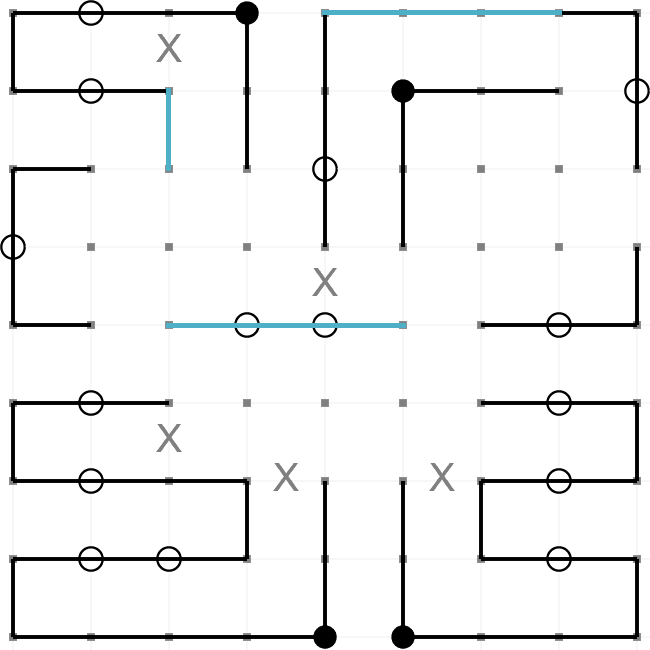
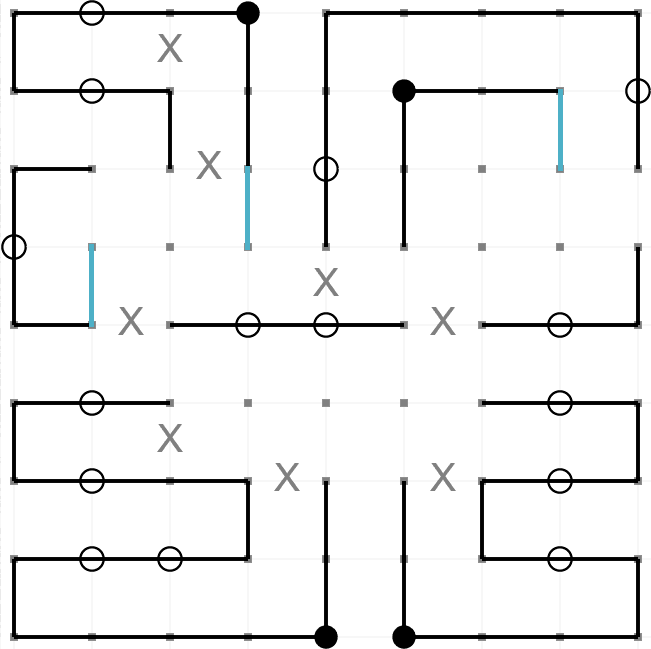
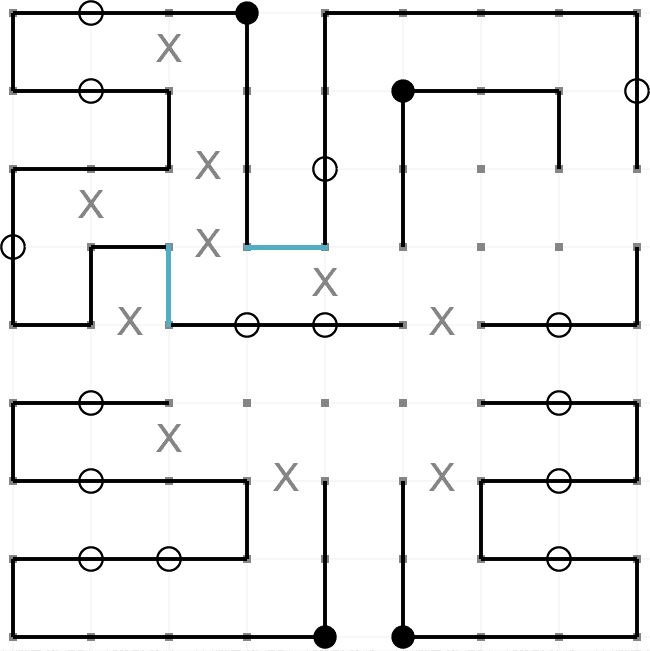
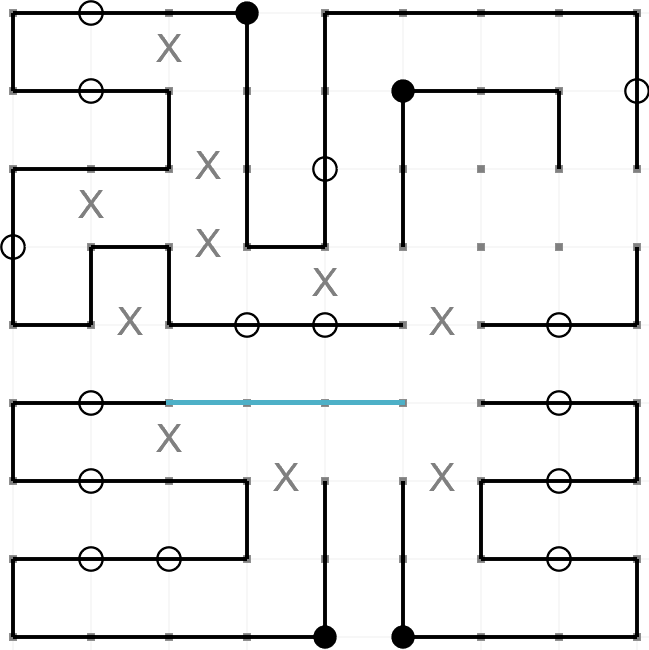
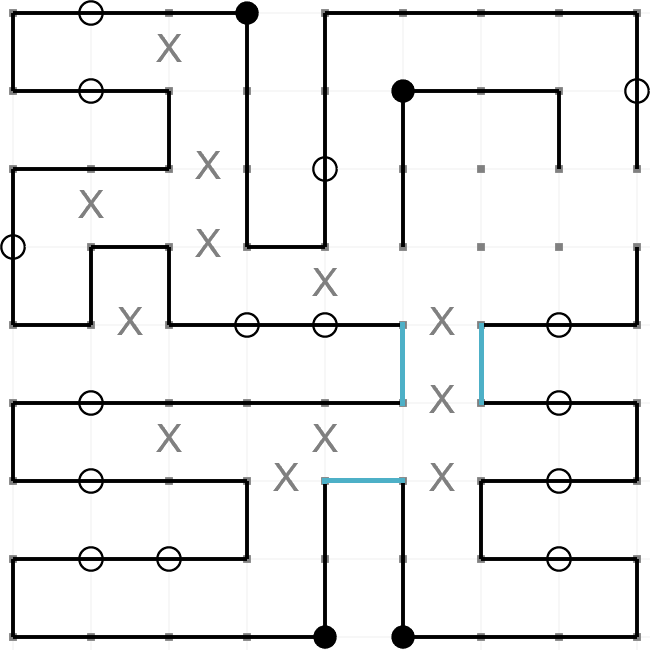
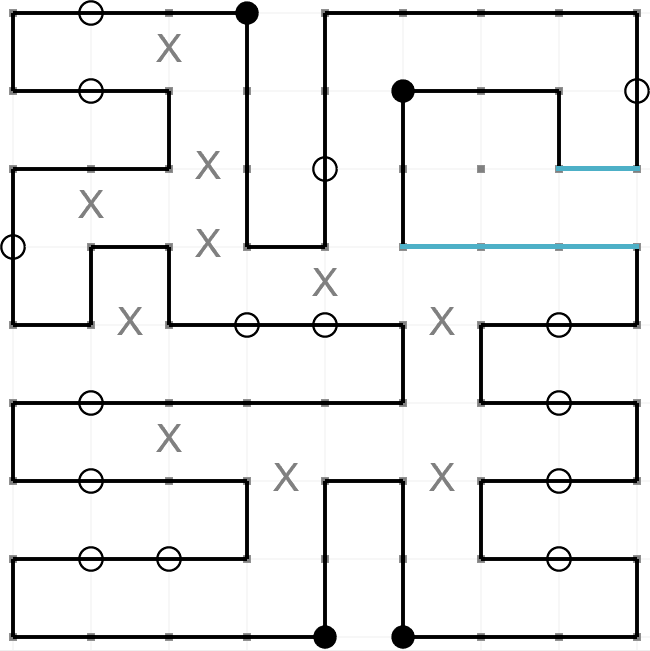
This is an example of a completed Masyu puzzle. The aim is to draw a path round the grid so that it
passes through every black and every white node. These are the rules,
- The path must turn on a black node. However, it must pass straight through the nodes before
and after.
- The path must pass straight through a white node. However, it must turn on one (or both)
of the nodes before and after.
 Masyu leaderboard
Masyu leaderboard