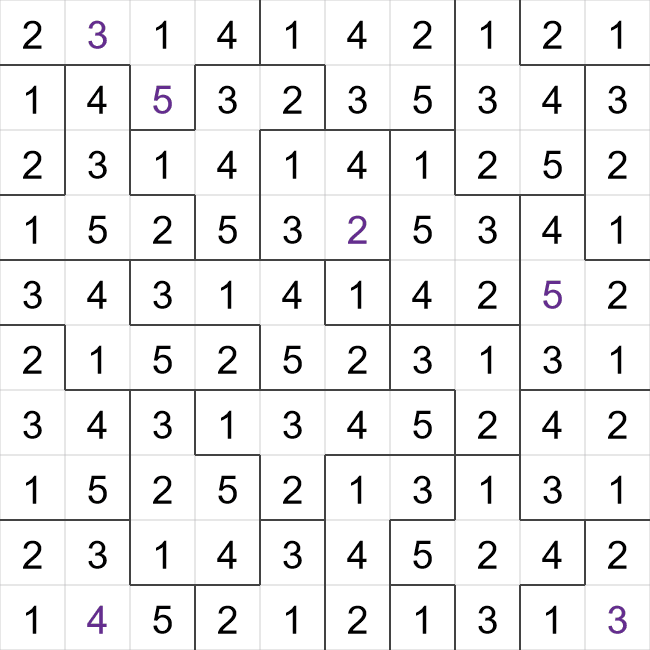
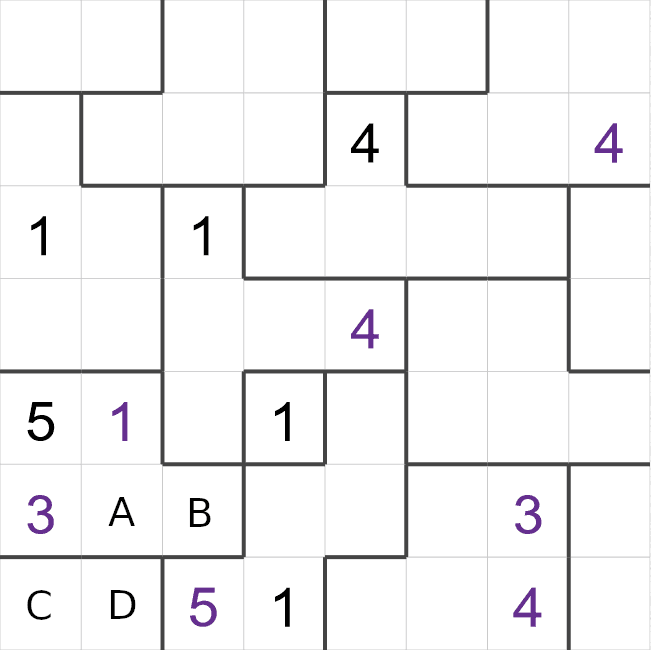
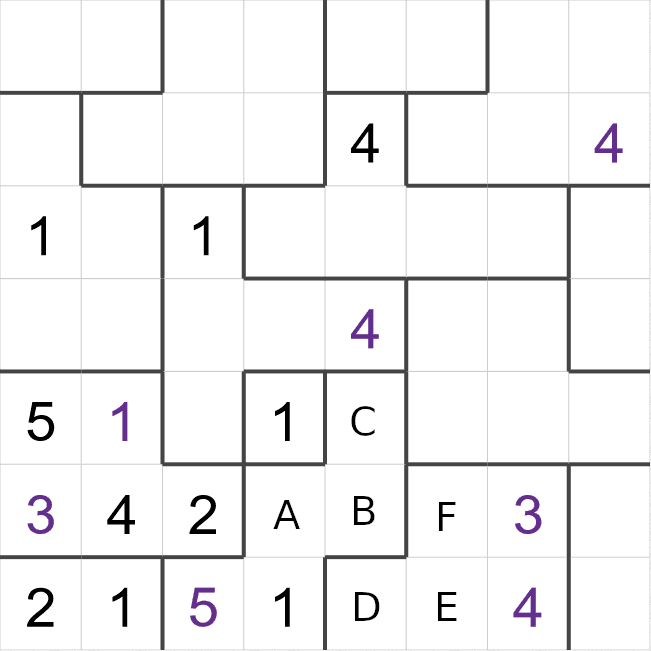
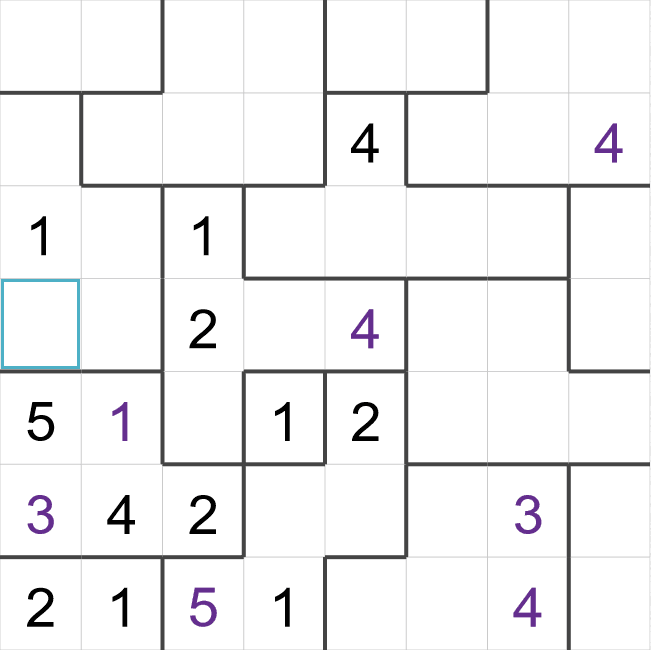
This is an example of a starting Suguru grid - some cells have been filled in already, but most are
empty.
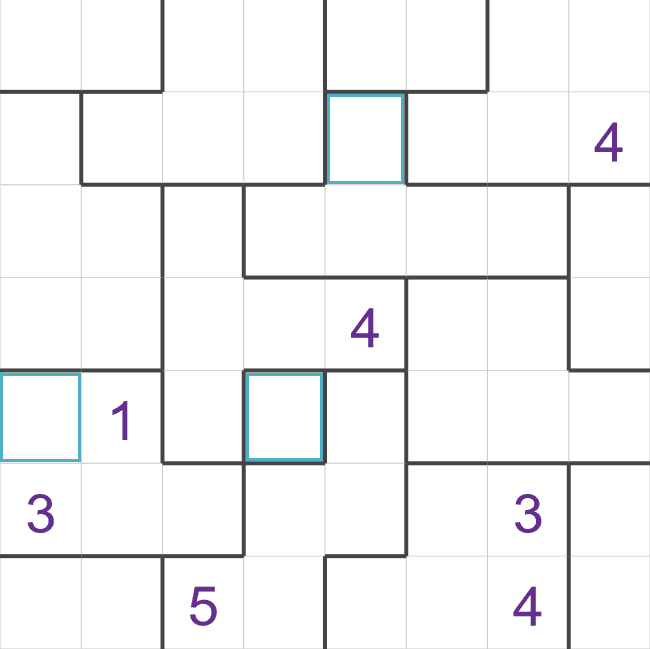
I have highlighted three cells here that we can fill in to begin with,
- This puzzle has a region with just one cell (in the center), this cell must be a 1. Most puzzles
don't have a region with just a single cell in this way, but this puzzle does!
- The cell on the left-hand side of the puzzle is in a region with 5 cells, so this region must
contain a '5'. The '5' must be in the highlighted cell because the other two empty cells are next
to the '5' on the bottom row.
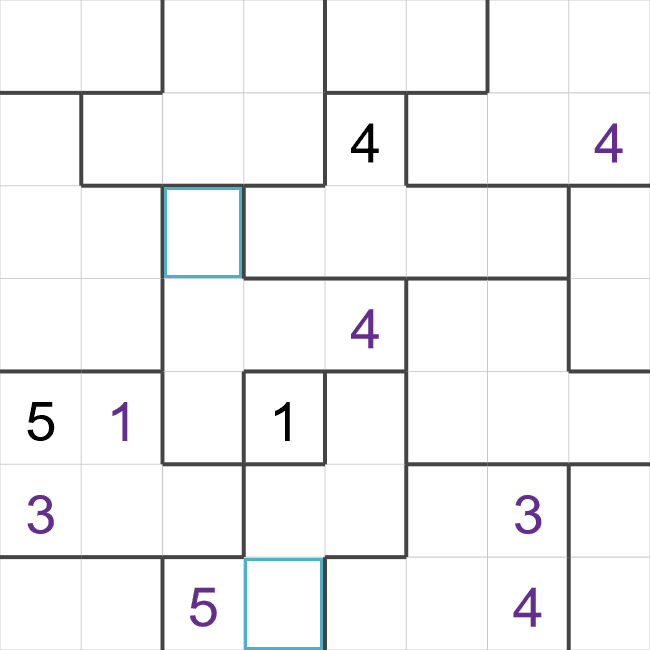
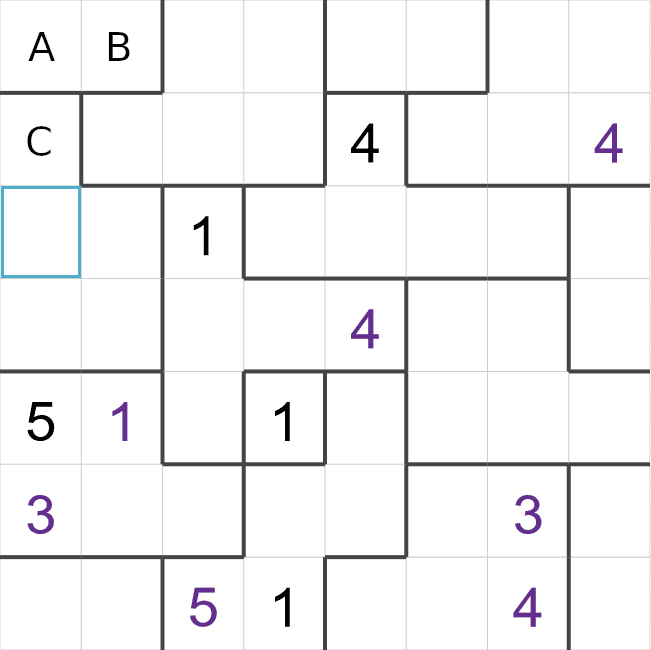
- The highlighted cells towards the top is in a region with 5 cells, so this region must contain
the numbers 1-5. The highlighted cell must be a '4'. All of the other cells are next to another
'4', remember that diagonals count as well!
 Suguru leaderboard
Suguru leaderboard