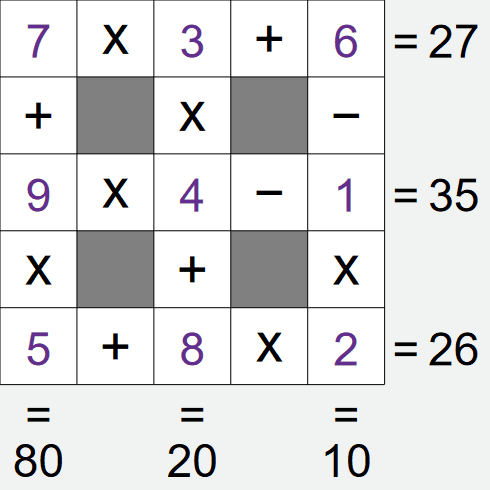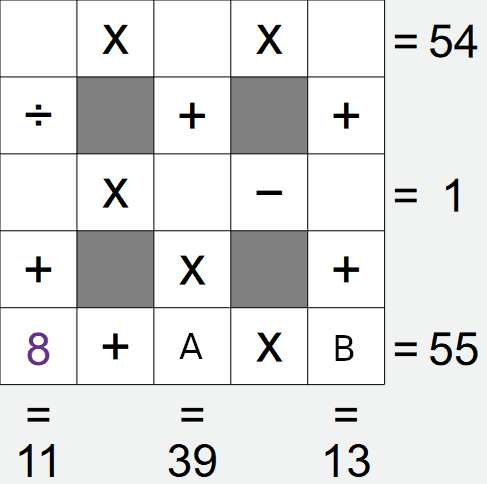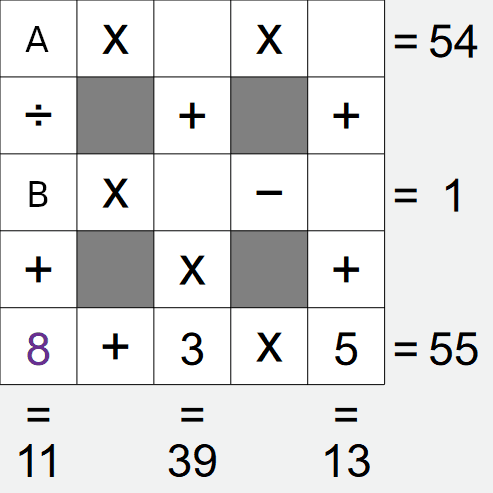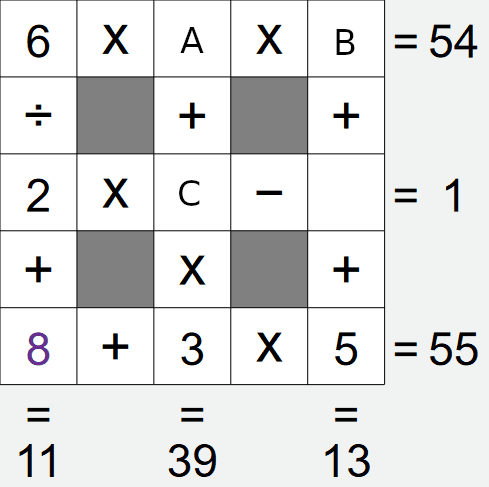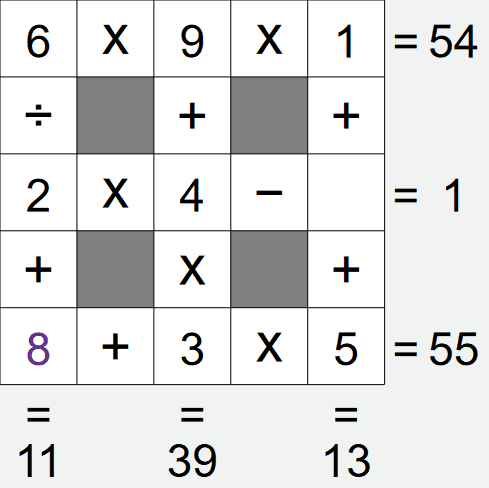This is an example of a completed SetSquare grid. The aim of this puzzle is to insert the numbers 1 to 9 (once and only once) in to the grid, so that the calculations are all satisfied.

Note that these calculations are done in left-to-right order, and not in PEMDAS/BIDMAS order. If we look at the calculation on the bottom row, we can see this in action, i.e. in left-to-right order this does give us the result of 26, but applying PEMDAS/BIDMAS rules would give 21.

This is an example of a SetSquare starting grid - depending on the difficulty level, we can be given a starting number. The best way to start a SetSquare puzzle is to look for calculations where there aren't that many possibilities.

Looking at the calculation on the bottom row, we have (8+A)xB = 55. We know that the only multiplications that give us 55 are 5x11 and 11x5. Cell B can't be 11 as this is not allowed by the rules. This means that cell B must be 5, and 8+A must be 11, i.e. A must be 3.

If we look at the left column, we have A÷B+8 = 11, i.e. A÷B = 3. Again, there is a limited number of ways we can satisfy this calculation,

1.    9 ÷ 3 = 3
2.    6 ÷ 2 = 3
3.    3 ÷ 1 = 3

We already have a 3 in this grid, this removes the first and last options, leaving only the second option left, i.e. cell A is 6, cell B is 2.

Looking at the top row, we have tha 6xAxB = 54. There is a limited number of ways we can satisfy this,

1.    6x9x1 = 54
2.    6x1x9 = 54
3.    6x3x3 = 54

We can remove the last option as this would mean that we have a '3' in the grid twice, which is not allowed. This means that cells A and B must be 1 and 9, we just don't know which order yet. At this point we would use pencil marks for this.

Looking at the middle column, we have (A+C)x3 = 39, i.e. A+C=13. Let's look at the different ways we can do this,

1.    4+9 = 13
2.    5+8 = 13
3.    6+7 = 13
4.    7+6 = 13
5.    8+5 = 13
6.    9+4 = 13

We can remove options 2, 3, 4, and 5 since that would mean using the same number twice. This leaves us with cells A and C being 4 and 9, we just don't know the order.

Combining both of these means that cell A must 9, cell B must 1, and cell C must 4.

The only number we are now missing is 7, and that completes this SetSquare puzzle!