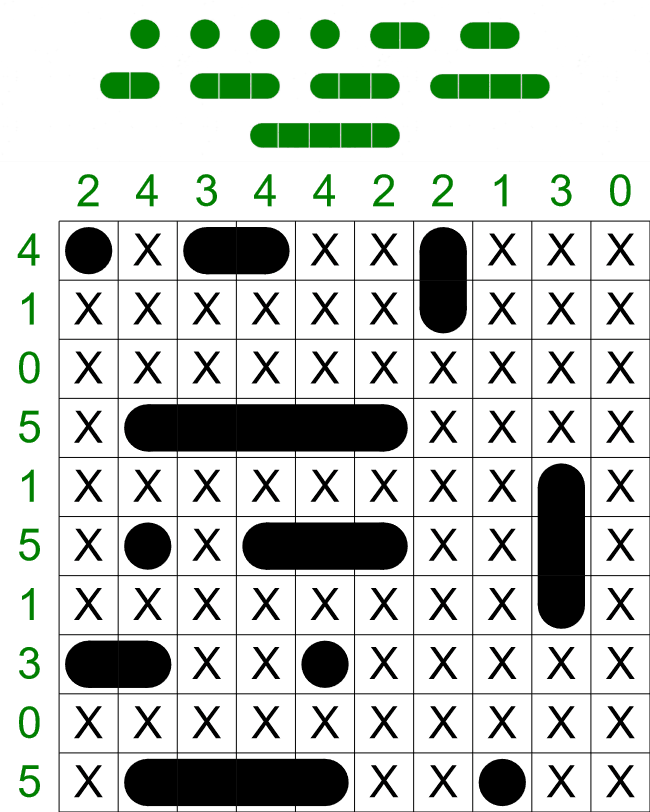
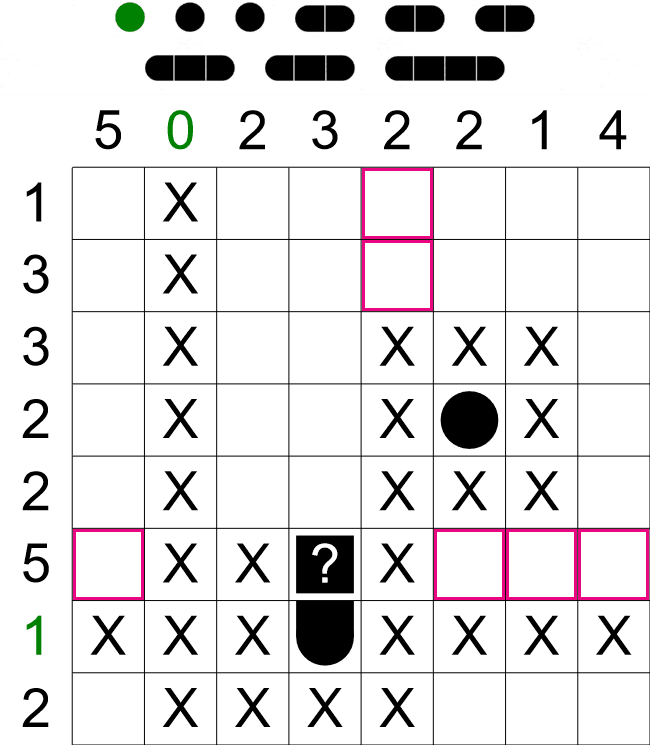
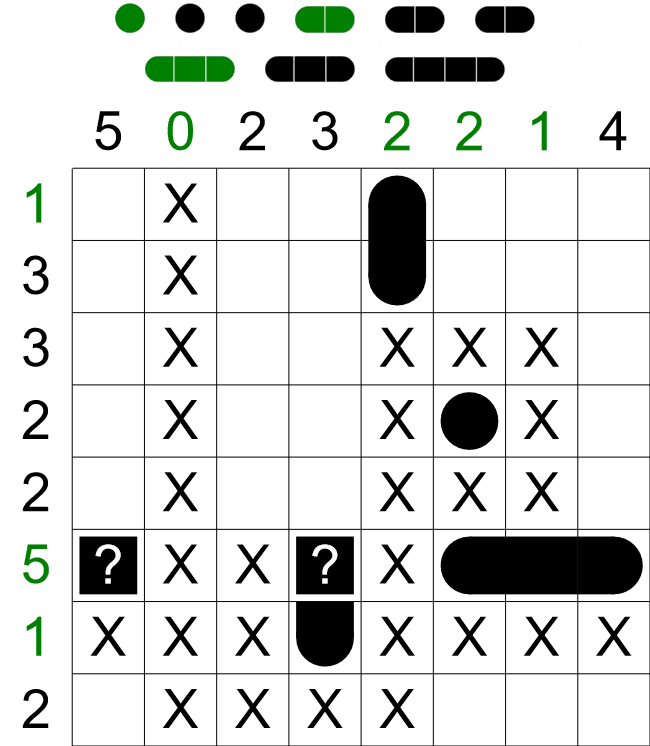
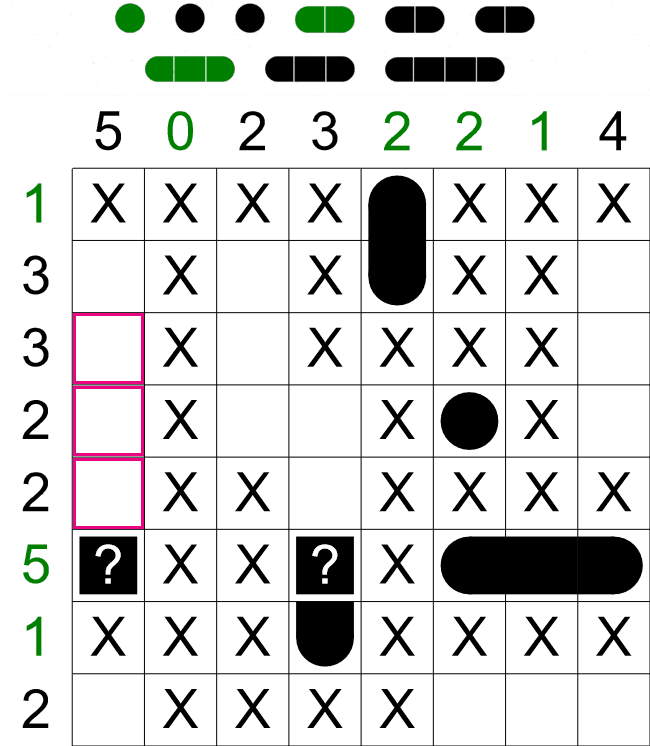
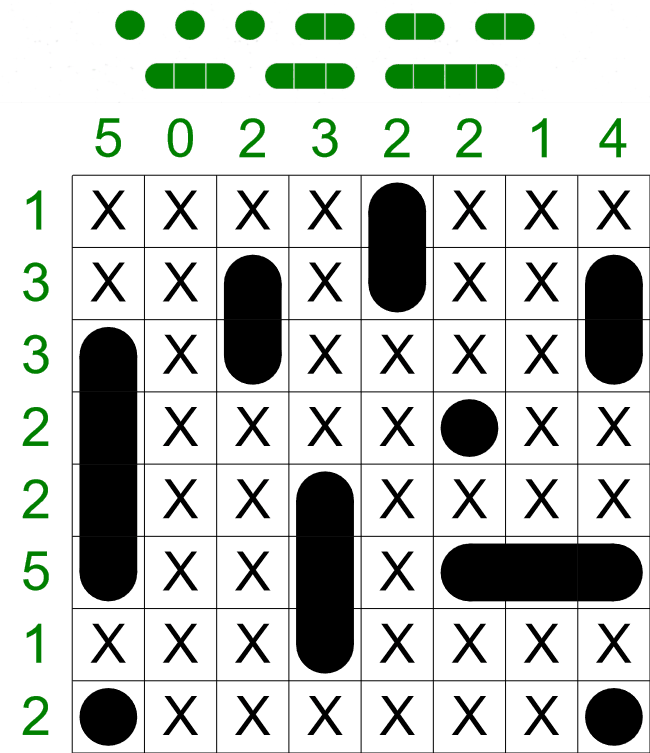
We have now progressed quite far on this puzzle, but we still have a long ship of 4 sections to fit in to
the grid somewhere. From looking at only the clues, there are three places this ship could go,
- The first column.
- The last column. This column already has one ship section, so this clue is effectively reduced
to '3', i.e. two low to contain a ship with 4 sections.
- The 6th row. This row is already filled with a combination of ships and empty cell, so we can
remove this possibility too.
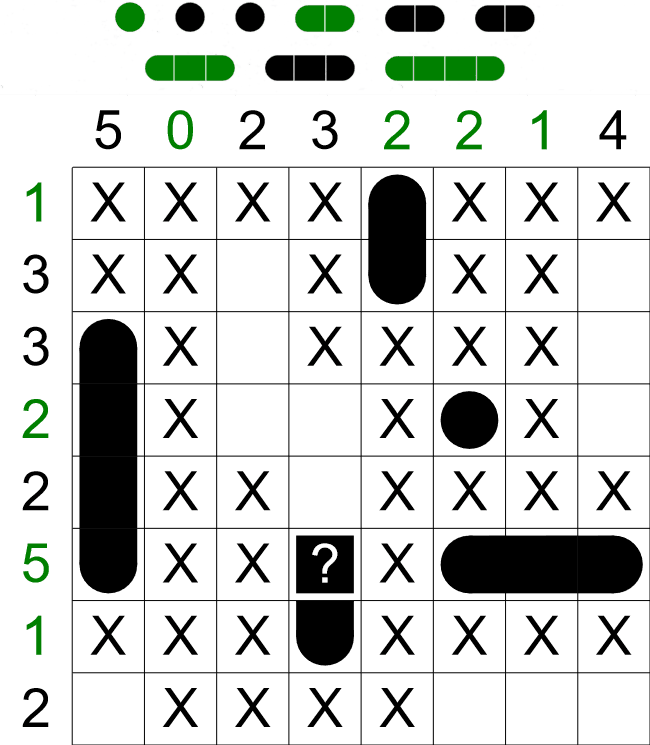
We already have one ship section in the first column, but the four other cells above it are free, so the
ship with 4 sections must fit in here in the highlighted cells. We can also mark the cell above this
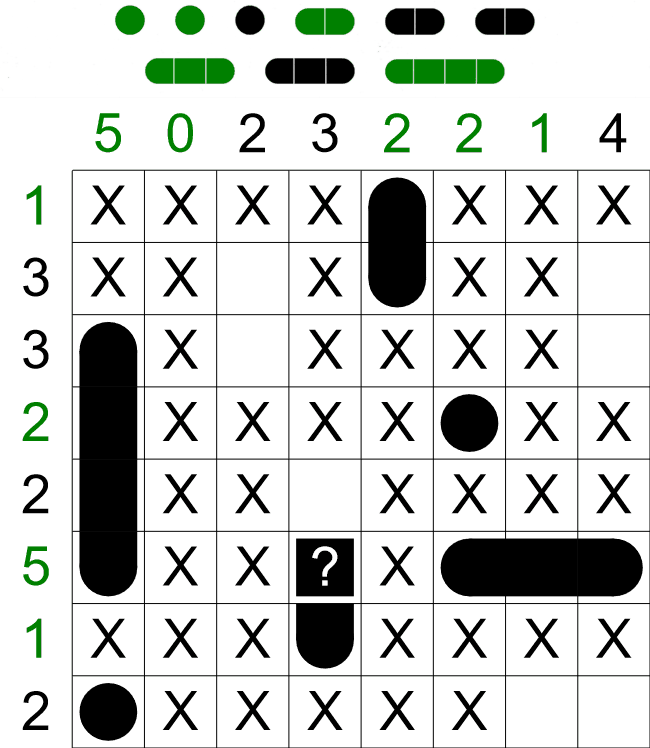
long ship as empty - this puzzle doesn't have ships with five sections, so it must be empty.
 Battleships leaderboard
Battleships leaderboard