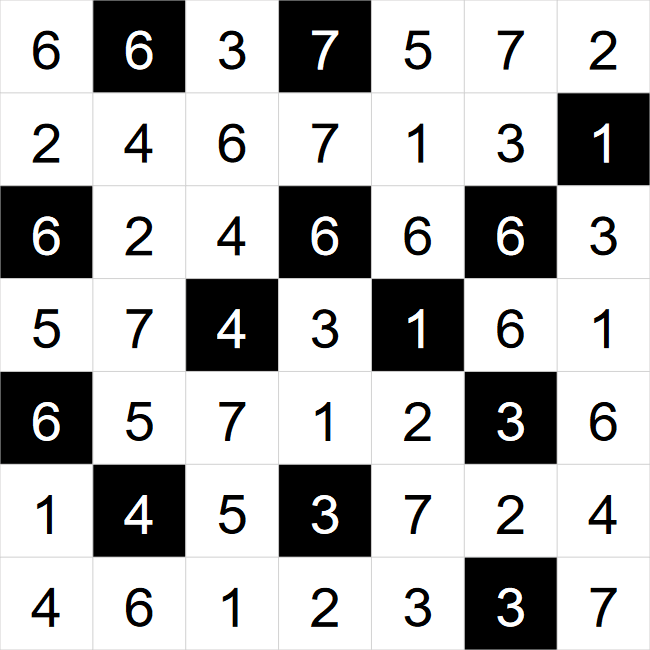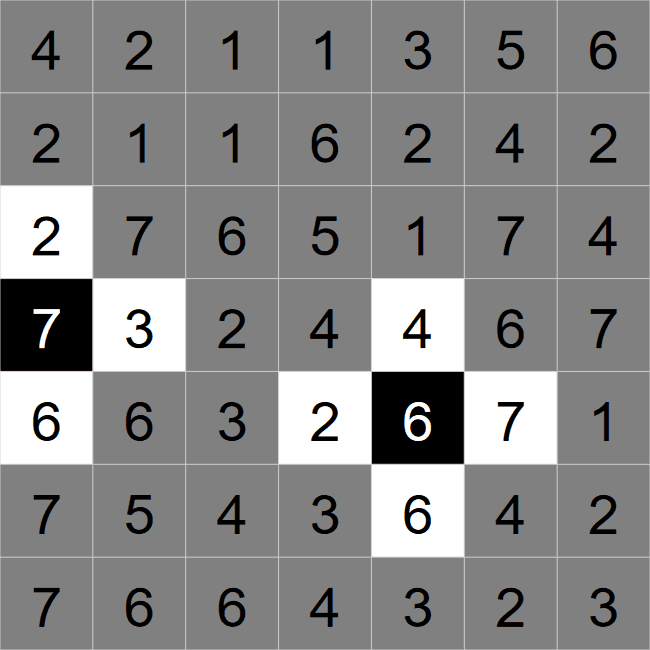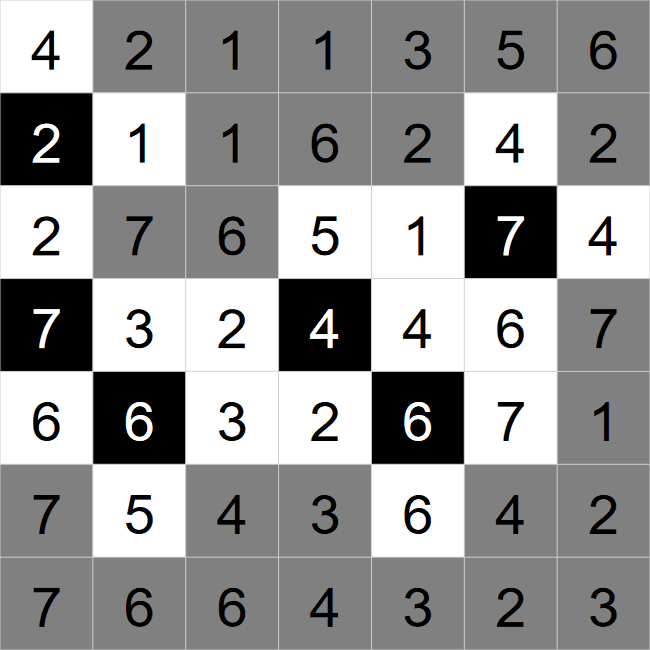This is an example of a starting grid. I have highlighted two cells that we can start with.
- Look at the left-most column. There are two 7s together at the bottom, since we can't have remove
both of these cells, one must be black, the other must be white. We don't know exactly which way round
(yet). Since we can only have one white number in each column, the highlighted 7 must be eliminated.
- We can apply the same technique to the highlighted 6, but by looking at the row instead.
We can also go a step further, since eliminated black cells can't touch any other eliminated black
cells, then all the cells around the 7 and the 6 must be white.
 Hitori leaderboard
Hitori leaderboard