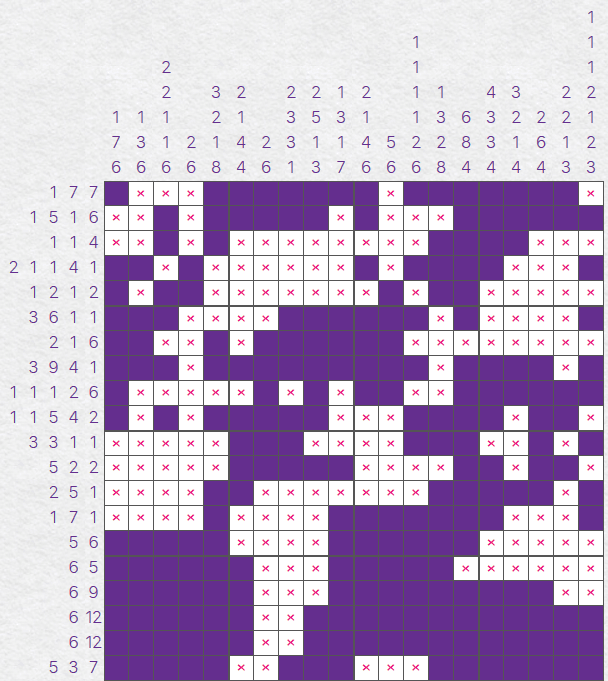
We now have this as our current work-in-progress. Notice that there is some overlap between the two
extremes in the middle of the grid, but that white cell in the middle is free to move between those two
extremes. It could also be more than just a single white square - all 4 white squares could be in the middle
for example.
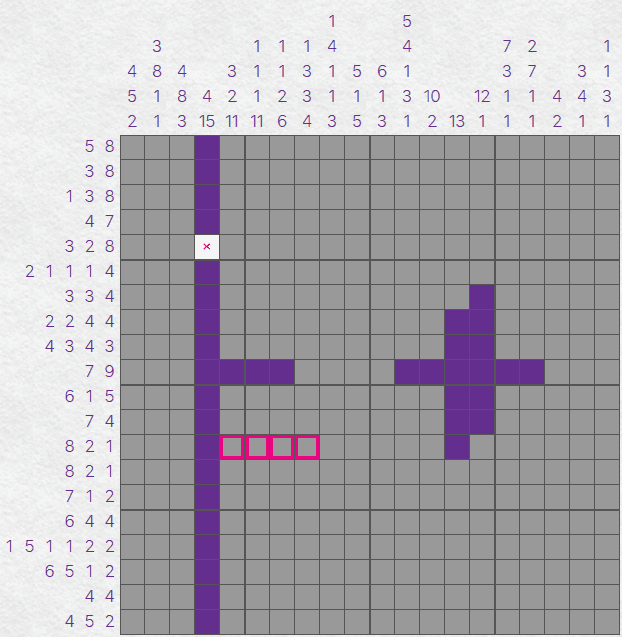
There's a few more opportunities for this kind thinking in this puzzle. We have three columns that are interesting
to us:
- The column with the clues of '4 15'.
- The column with the single clue of '13'.
- The column with the clue of '12 1'.
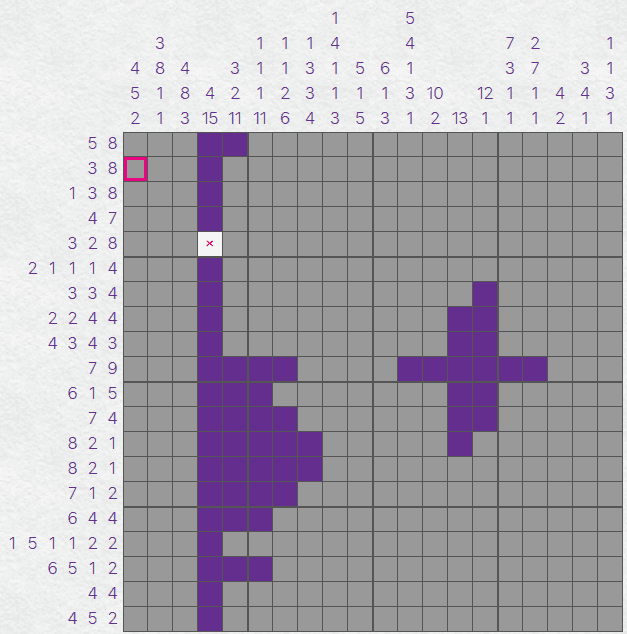
You may notice that there is only one way to satisfy the first of our columns - so we can completely
fill that column in. We can also apply the same process to our other two columns.