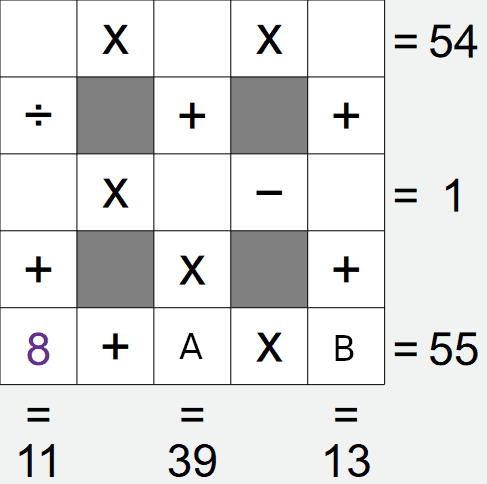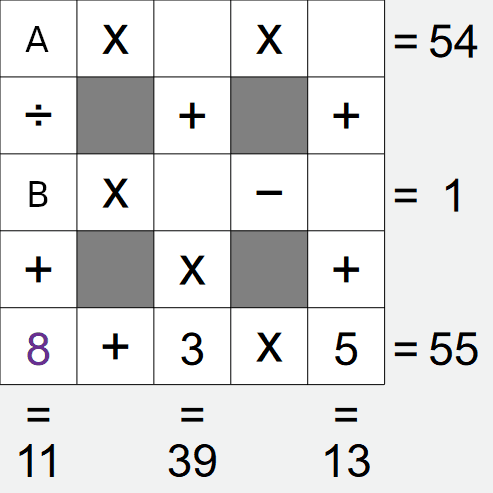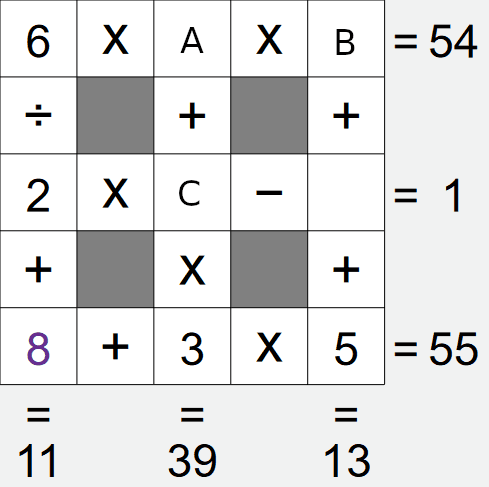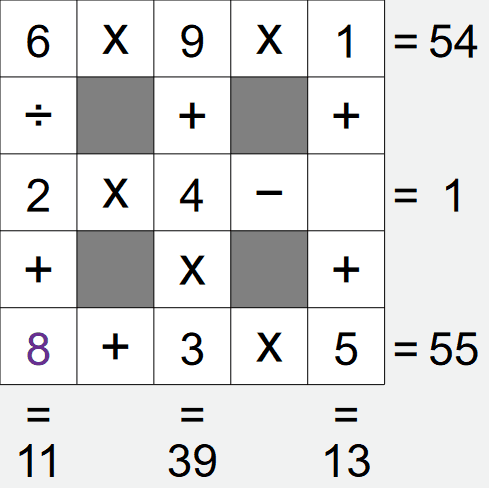If we look at the left column, we have A÷B+8 = 11, i.e. A÷B = 3. Again, there is a limited
number of ways we can satisfy this calculation,
- 9 ÷ 3 = 3
- 6 ÷ 2 = 3
- 3 ÷ 1 = 3
We already have a 3 in this grid, this removes the first and last options, leaving only the second
option left, i.e. cell A is 6, cell B is 2.
 SetSquare leaderboard
SetSquare leaderboard