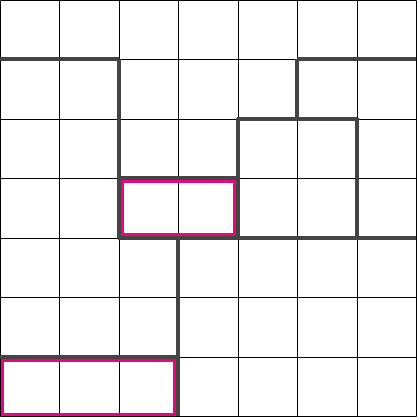
This is an example of a starting grid requiring two stars in each row/column/region. These puzzles are
a little harder, but the overall approach is the same. We have two regions that are only a single
cell in height. We know that these regions must contain two stars, which means none of the other
cells in that row can contain any stars.
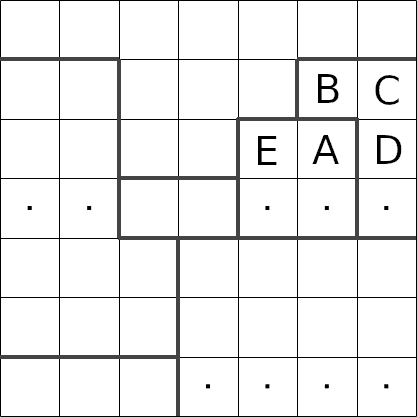
In fact, for the rectangle in the middle of this puzzle, there is only one way we can insert two stars
in there, i.e. in cells 'A' and 'B'.
We can also look at cell 'C'. This cell is in the middle of a small region. If we were to insert a
star in here, there would be no more free cells for the other star, i.e. cell 'C' must be empty.
 Star Battle leaderboard
Star Battle leaderboard