Suko leaderboard
Suko leaderboard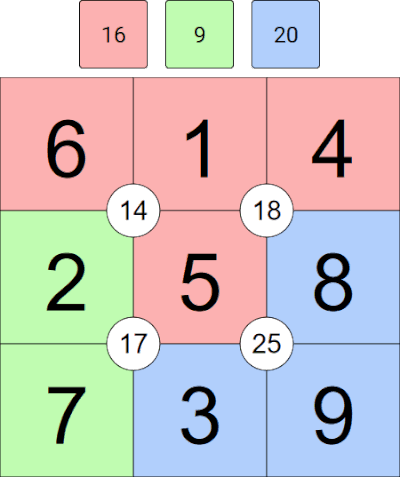
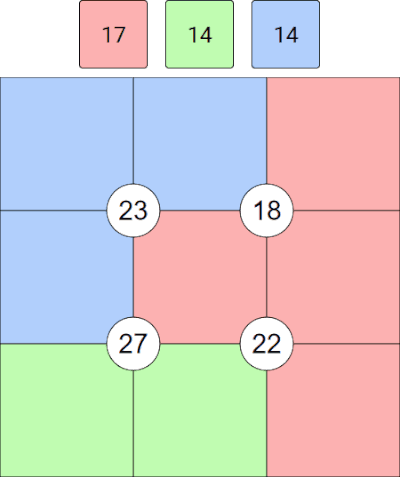
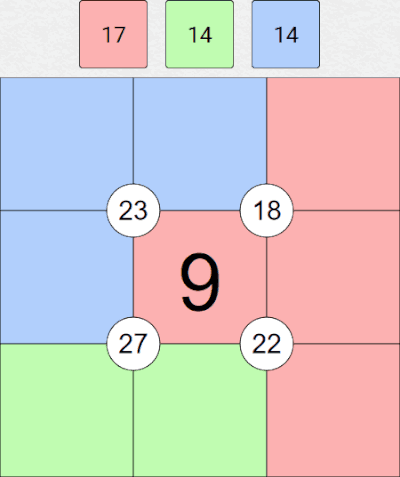
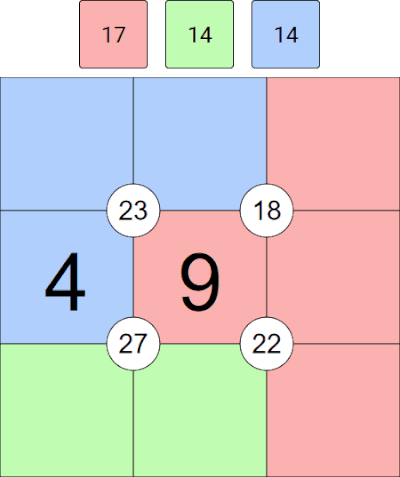
Quadrant totals: These are the numbers given in the circles inside the grid itself. The quadrant total in the top-left is 14, for example. We can add the 4 cells around this total together, 6+1+2+5, to check that we get 14.
We can do the same thing for the lower-right quadrant total of 25, i.e. 5+8+3+9 to make sure that gives us 25.
Layout totals: There will always be three different colours for the cells in each puzzle. The numbers above the grid tell you what these should add to. From this puzzle, we can see that,