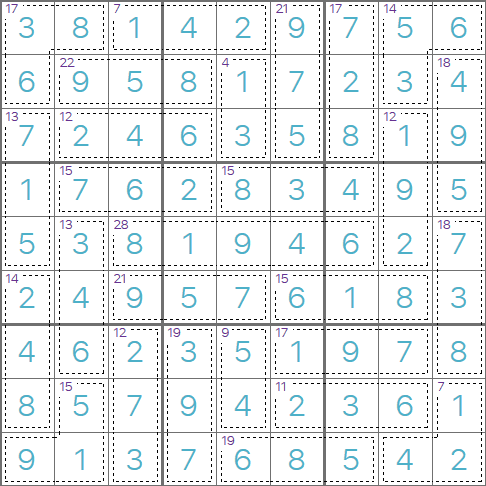
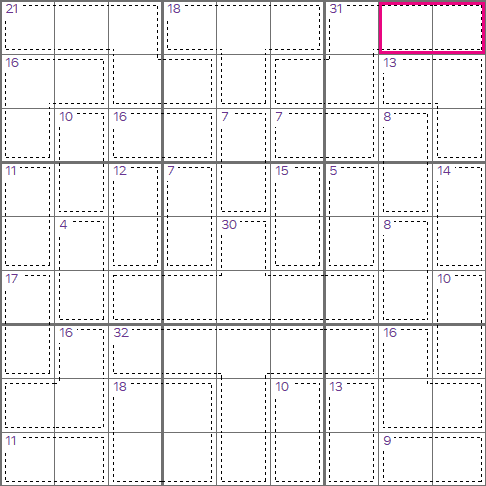
This is a Killer Sudoku starting grid, the first thing you'll need notice is that there are no starting
numbers! We need to use a different set of techniques to get started with Killer Sudoku puzzles. We know
that each row column and 3x3 region will contain the numbers 1-9, if we add these together we get
1+2+3+4+5+6+7+8+9=45, i.e. each row, column, and 3x3 region must add to 45/
Look at the bottom-right 3x3 region, we have 4 cages that add to 16+7+10+4=37. These cages between them
cover 8 out of the 9 cells in this region. That means the remaining (highlighted) cell must be 45-37=8.
This is a great technique to use when starting with Killer Sudoku grids. You will also use techniques
that you might use for Mathdoku puzzles. For example, the cage with 2 cells adding to 4 in the bottom-right
only has one combination, i.e. 1+3=4. We can pencil these in and use the naked pairs technique.
 Killer Sudoku leaderboard
Killer Sudoku leaderboard