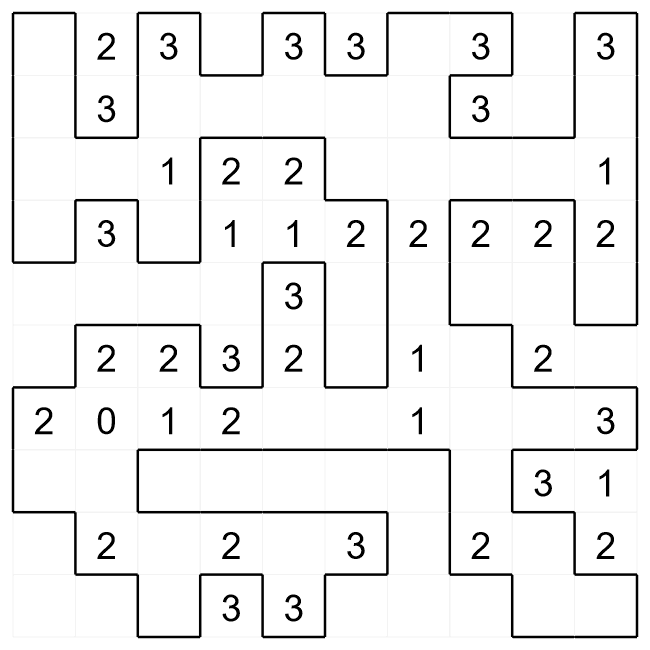
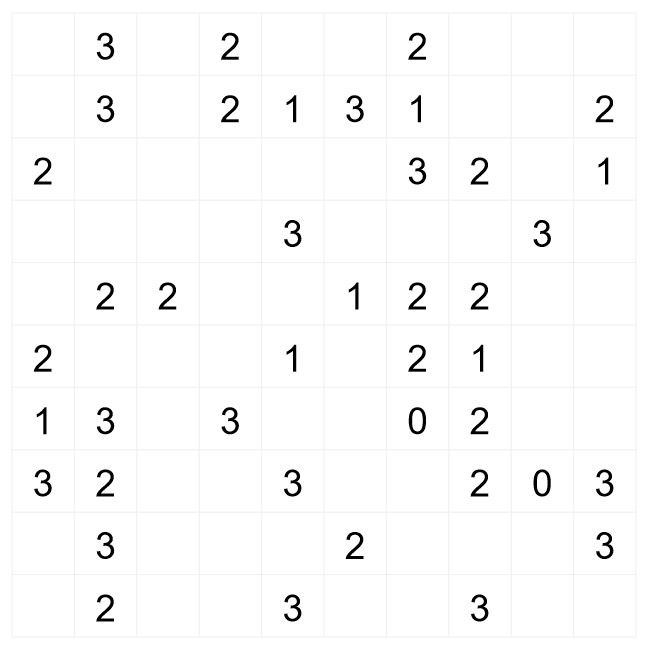
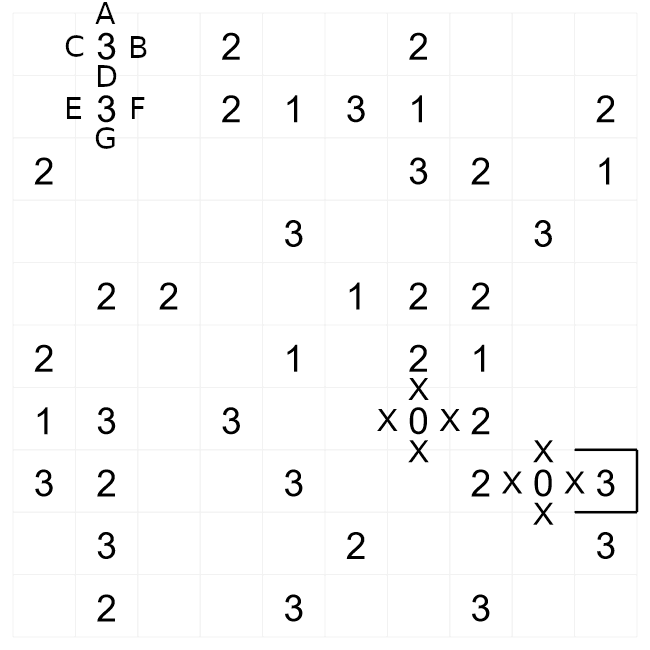
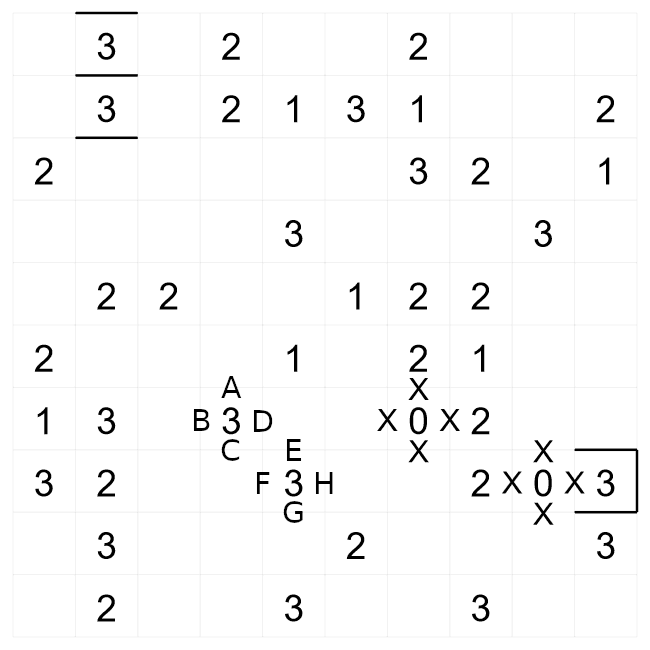
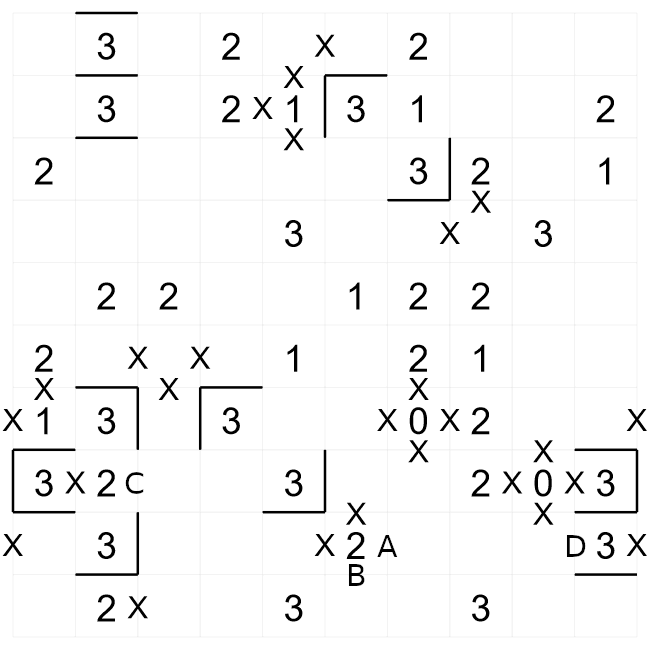
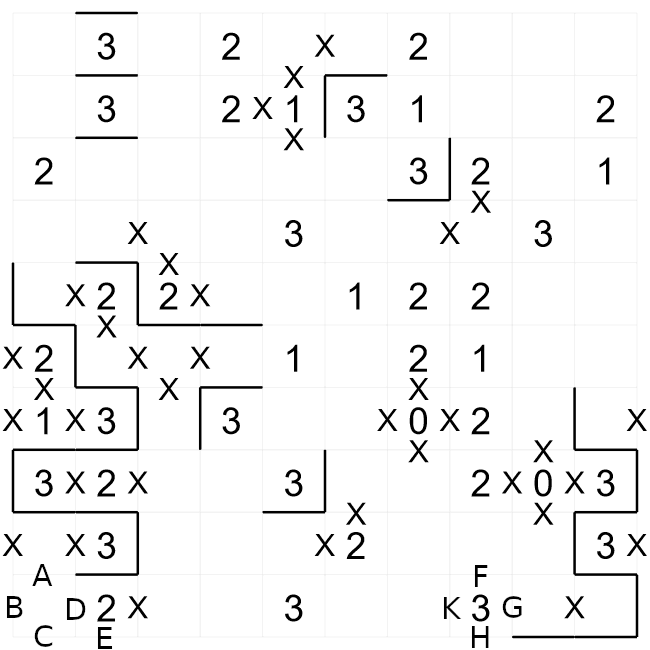
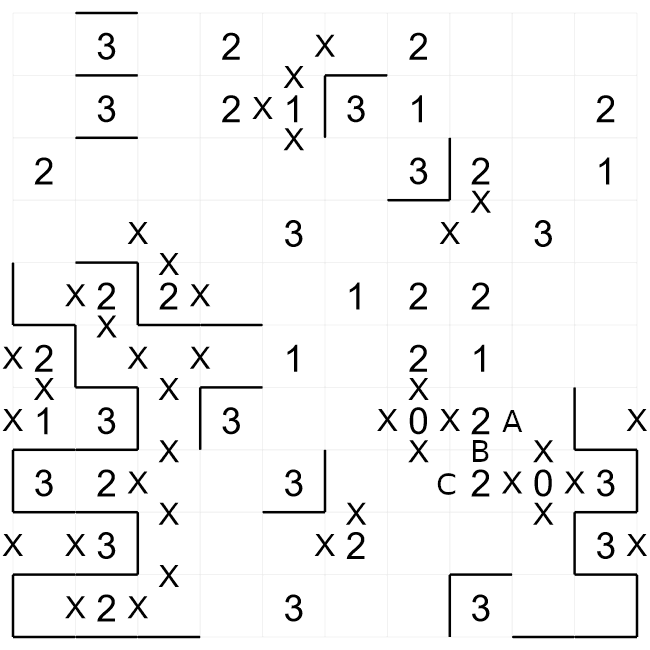
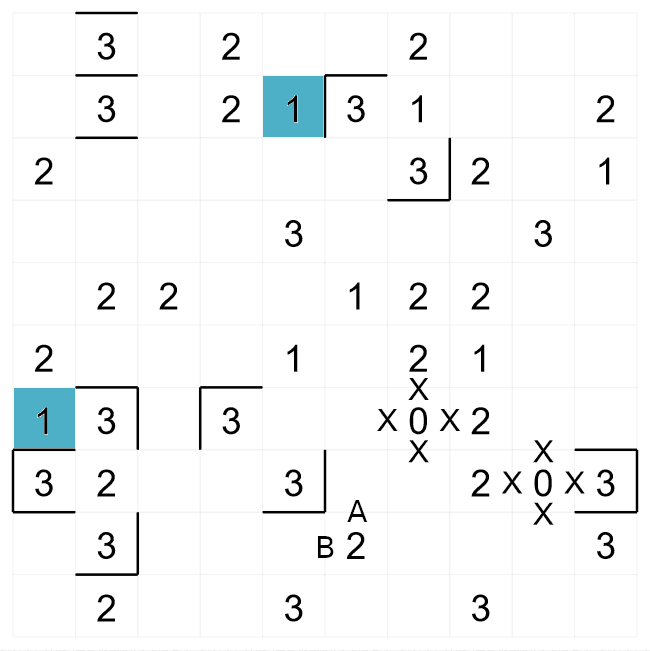We have now made more progress on this puzzle by continuing to apply the same logic of where walls
can go, and where they can't go. Now consider the area in the bottom-left of this puzzle. The wall
must exit this area in this way. There are two possibilities, it can either exit via ABCE, or go
directly with DE. If it follows DE, then the '2' clue will have three surrounding walls, so that
can't be possibility, so the wall must follow the ABCE path.
The '3' clue towards the bottom-right has the wall approaching from the right. There are only two
ways the wall can satisfy the '3' clue from here, either HKF, or GFK. Both of the possibilities have
F and K as walls, so we can fill these in.
 SlitherLink leaderboard
SlitherLink leaderboard