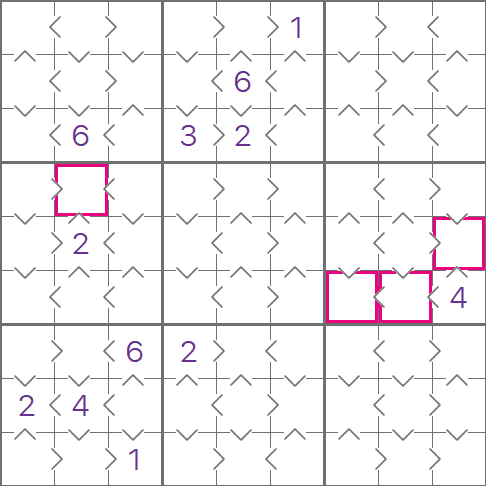
This is an example of an easy starting grid, we have been given some starting numbers, and we have a full
set of relationships between cells.
I have highlighted a cell on the left, there is a '2' in the cell below, and we know from the ^ that the
highlighted cell must be smaller, so the hilighted cell must be a '1'. There is another '1' we can insert
in to this grid, try to find it!
I have also highlighted three cells on the right-hand side of this grid. We can't insert any numbers here,
but all three cells are smaller than 4, and there are exactly 3 numbers smaller than 4. This means we
know that these cells must contain the numbers 1, 2 and 3, we don't know the exact placement, but we can
insert some pencil marks.
We can also insert a '3' in the bottom-left 3x3 region, try to find where!
 Greater Than Sudoku leaderboard
Greater Than Sudoku leaderboard